في هذا الدرس سنركز على فهم ماهية البيانات المنحرفة وكيفية التعامل معها إن وجدت في مجموعة بياناتك، ومدى تأثيرها على رؤيتك الإحصائية التي تريد تحقيقها باستخدام نموذجك الإحصائي أو نموذج التعلم الآلي الذي ستقوم بتطويره لحل مسألة ما، كالمسائل المتعلقة بخوارزميات الانحدار Regression Algorithms.

توصف البيانات بأنها بيانات منحرفة Skewed Data عندما يكون المنحنى الممثِّل للبيانات في التوزيع الإحصائي Statistical Distribution مُشوَهًا أو مُنحرفًا إما إلى اليسار أو إلى اليمين.

في المقابل يوجد مايسمى بالتوزيع الطبيعي Normal Distribution أو التوزيع المتماثل Symmetric Distribution ، حيث يُظْهِر الرسم البياني تماثلاً مما يعني وجود العديد من قيم البيانات على الجانب الأيسر من الوسيط median كما هو الحال في الجانب الأيمن. الشكل 1.1

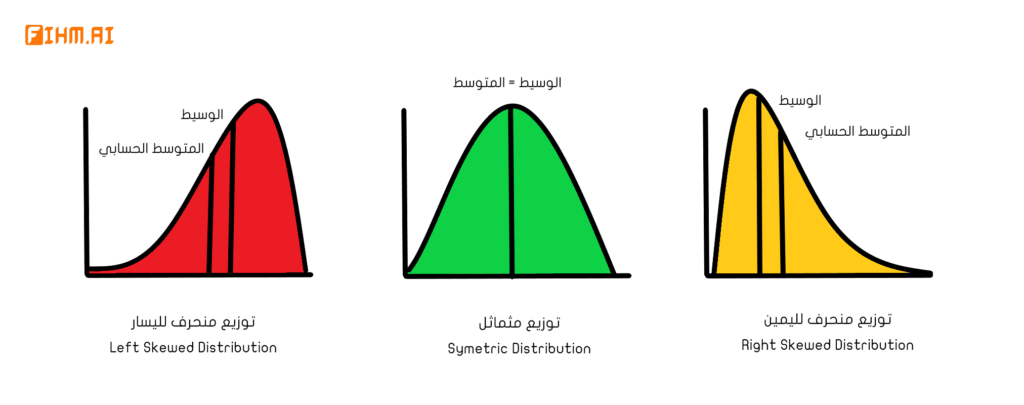
قبل الشروع بتفصيل هذه التوزيعات الإحصائية سنراجع سوية بعض المصطلحات الإحصائية المهمة:

• المنوال Mode: هو أكثر قمية متكررة في مجموعة البيانات.
• المدى Range: هو الفرق بين أكبر قمية و أصغر قيمة في مجموعة البيانات.
• الوسيط Median: هو القيمة التي تقع في وسط مجموعة من البيانات مرتبة ترتيبًا تصاعديًا من الأصغر إلى الأكبر.
• المتوسط الحسابي (المعدل) Mean: هو مجموع القيم الموجودة في مجموعة البيانات مقسومًا على عددها.

تعد هذه القيم الإحصائية مؤشرًا ومقياسًا لتحديد تمركز البيانات في التوزيع الإحصائي حيث أنها تحدد مدى إنحراف هذه البيانات ، فعلى سبيل المثال في التوزيع الطبيعي يكون كل من المنوال ، الوسيط ، والمتوسط الحسابي قيمًا متقاربة جداً من بعضها بينما في التوزيعات المنحرفة تكون هذه القيم متباعدة عن بعضها البعض كما سيتم توضيحه في الأسطر القادمة.

التوزيع المنحرف ناحية اليمين | Right Skewed Distribution

هذا التوزيع يسمى أيضًا بالتوزيع إيجابي الانحراف Positive Skewed حيث تكون البيانات منحرفة باتجاه اليمين ويتكون مايشبه الذيل الطويل في اتجاه المحور الموجب لـ x للدلالة على حدوث الانحراف في البيانات كما هو موضح في الشكل 1.2 أدناه.

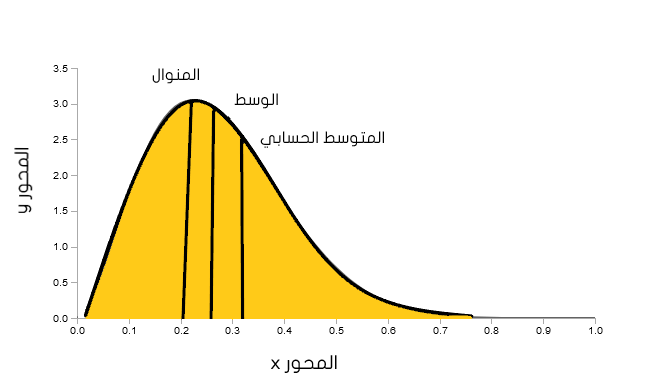
خصائص التوزيع :

• المتوسط الحسابي > المنوال
• الوسط > المنوال
• المتوسط الحسابي > الوسط

تعد كل من العبارة الأولى والثانية صحيحة دائمًا في التوزيعات المنحرفة إلى اليمين ولكن العبارة الثالثة ليست بالضرروة كذلك حيث أن التوزيعات الإنحرافية تأخذ أشكالًا متعددة.

التوزيع المنحرف ناحية اليسار | Left Skewed Distribution

يسمى أيضًا بالتوزيع سلبي الانحراف Negative Skewed حيث تكون البيانات منحرفة باتجاه اليسار وكما هو الحال مع الإنحراف الإيجابي يتكون مايشبه الذيل الطويل في اتجاه نقطة الأصل أو المحور السالب لـ x كما هو موضح في الشكل 1.3 أدناه.

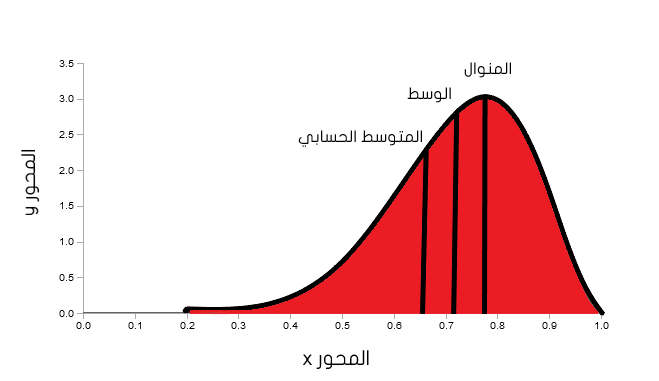
خصائص التوزيع :

• المتوسط الحسابي < المنوال
• الوسط < المنوال
• المتوسط الحسابي < الوسط

كما هو الحال مع التوزيع السابق تعد كل من العبارة الأولى والثانية صحيحة دائمًا في التوزيعات المنحرفة إلى اليسار ولكن العبارة الثالثة ليست بالضرورة أن تكون صحيحة.

تأثير الإنحراف على النماذج | Effect of Skewness on models

عادة ما تكون التوزيعات الواقعية للبيانات منحرفة ، وإذا ما كان هنالك انحراف كبير في البيانات ، فإن العديد من النماذج الإحصائية لن تعمل بشكل صحيح ولكن لماذا ؟!

ذكرنا أن التوزيعات المنحرفة تتكون في تمثيلها من ذيل طويل والذي يعتبر بدوره بمثابة قيم متطرفة Outliers في البيانات وكما نعلم فإن القيم المتطرفة تؤثر سلبًا على أداء النموذج المراد تطويره على هذه البيانات وبالخصوص النماذج المبنية على مسائل الانحدار Regression، ولكن على صعيد آخر فإن النماذج المبنية على شجيرات القرارات Tree-Based Models تعتبر أقوى من حيث التعامل مع هذه القيم المتطرفة ولكنها ستحد من استخدام نماذج أخرى لذلك ينبغي تحويل أو مقاربة هذه البيانات إلى توزيع غاوسي Gaussian Distribution أو توزيع طبيعي Normal Distribution لتلافي هذه المشكلة.

تطبيق عملي | Practical Implementation

بالإمكان تحميل كل من الـ Notebook و البيانات المستخدمة عبر النقر على الرابط 🔗 لتجربة الأكواد بنفسك:

سنقوم بالعمل على بيانات مخصصة لتوقع أسعار السيارات حسب عدة ميزات تتضمنها هذه السيارات وسنركز فقط على الميزات الرقمية Numerical Features للتحقق من التوزيعات الإحصائية ووجود أي انحرافات في البيانات لتقويمها.

1- استدعاء المكتبات:

2- سحب البيانات:

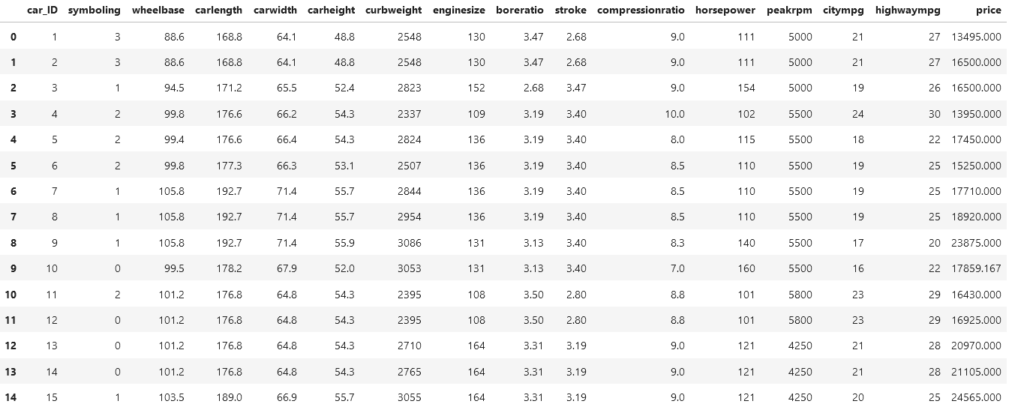
الآن سنركز على بعض الميزات فقط (الأعمدة) ونقوم بفحص البيانات للتأكد من توزيعها الاحصائي وذلك عن طريق رسم مدراج التكرارات Histogram Graph

3- التأكد من التوزيع الاحصائي للبيانات

لنأخذ على سبيل المثال ميزة سعة محرك السيارة ونشاهد التوزيع الاحصائي لهذه الميزة:

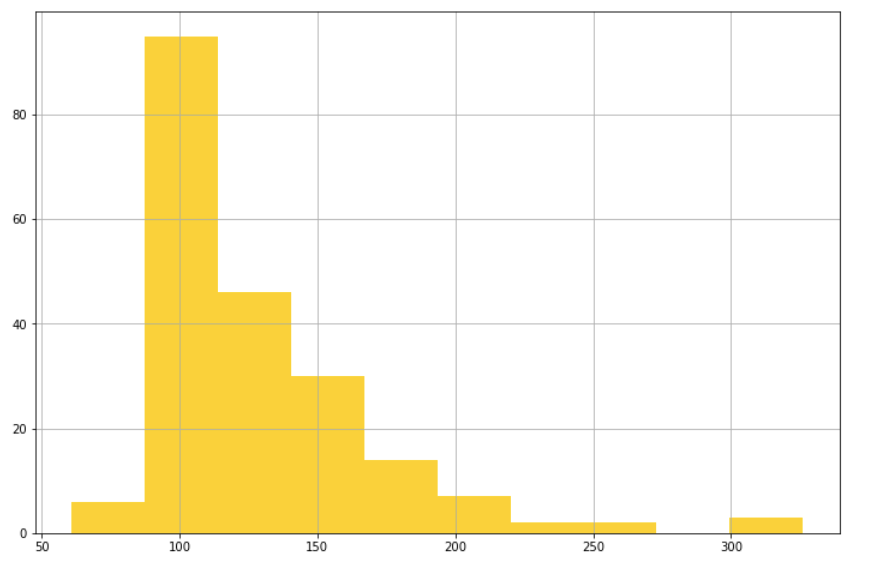
نلاحظ بوضوح أن الرسم لا يشكل توزيعًا طبيعيًا بل يشكل توزيعًا منحرفًا ناحية اليمين ! سنستخدم طريقة احصائية أخرى للتأكد من وجود الانحراف وهو مايسمى باختبار داجوستينو D’Agostino K^2 Test من خلال ما يسمى بقيمة P أو P-value حيث تعد هذه القيمة مؤشرًا على ميل البيانات لتمثيل توزيع طبيعي بحيث كلما كانت هذه القيمة أعلى كلما كانت البيانت موزعة بشكل طبيعي أكثر ويحدد الإحصائيون في العادة قيمًا مختلفة لـ P لقبول مثل هذه الفرضيات ولن ندخل في تشعبات هذا الأمر بل سنعتمد ما يلي:

عندما تكون P > 0.05  فهذا يقتضي توزيعًا طبيعياً    

الآن سنجرب ذلك برمجيًا من خلال مكتبة SciPy عبر دالة normalist

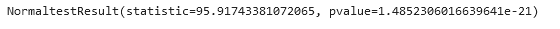
الذي نلاحظه أن قيمة الـ p-value صغيرة جداً حيث أنها تساوي = p-value = 1.485 x 10 ^ -21 وهذا يعني أنها بعيدة تمامًا عن كونها تمثل توزيعًا طبيعيًا للبييانات!

4- التعامل مع المشكلة

سنستخدم ثلاث أساليب مختلفة للتعامل مع هذا التوزيع لمحاولة تحويله إلى ما يشبه التوزيع الطبيعي :

• التحويل اللوغاريتمي | Log Transformation
• التحويل بالجذر التربيعي | Square Root Transformation
• التحويل بصندوق كوكس | Cox Box Transformation

أولًا التحويل اللوغاريتمي

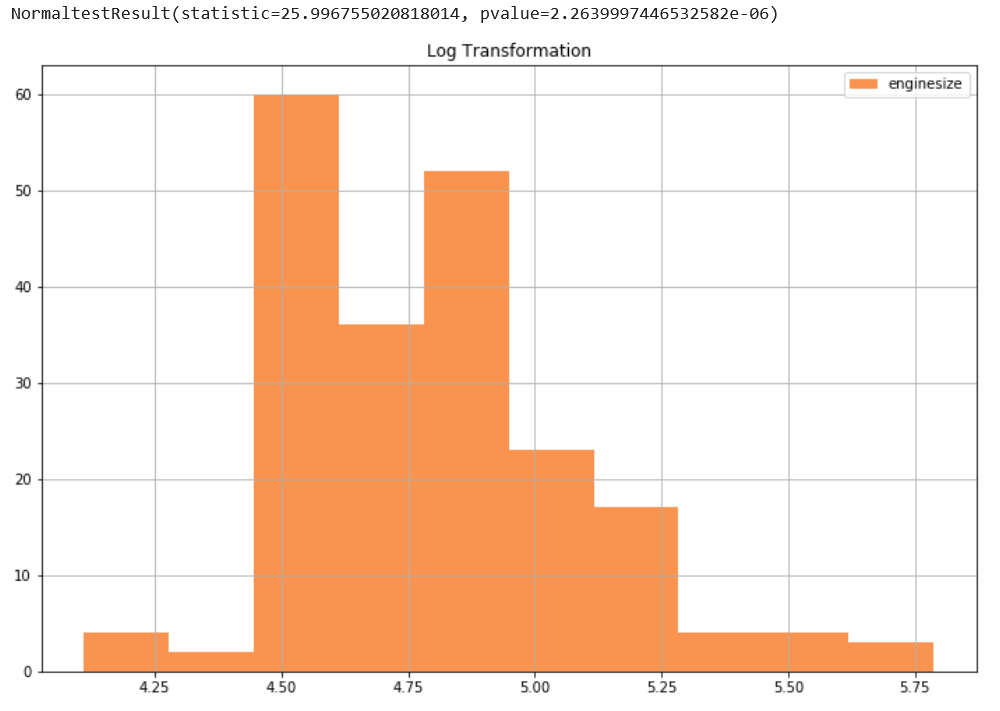
نلاحظ أن البيانات بعد التحويل قد اقترتب من التوزيع الطبيعي وقيمة P تحسنت بشكل كبير p-value = 2.26 x 10^-6 ولكن لازالت لا تمثل توزيعًا طبيعيًا حسب المعيار الذي وضعناه في الأعلى!

ثانيًا : التحويل بالجذر التربيعي

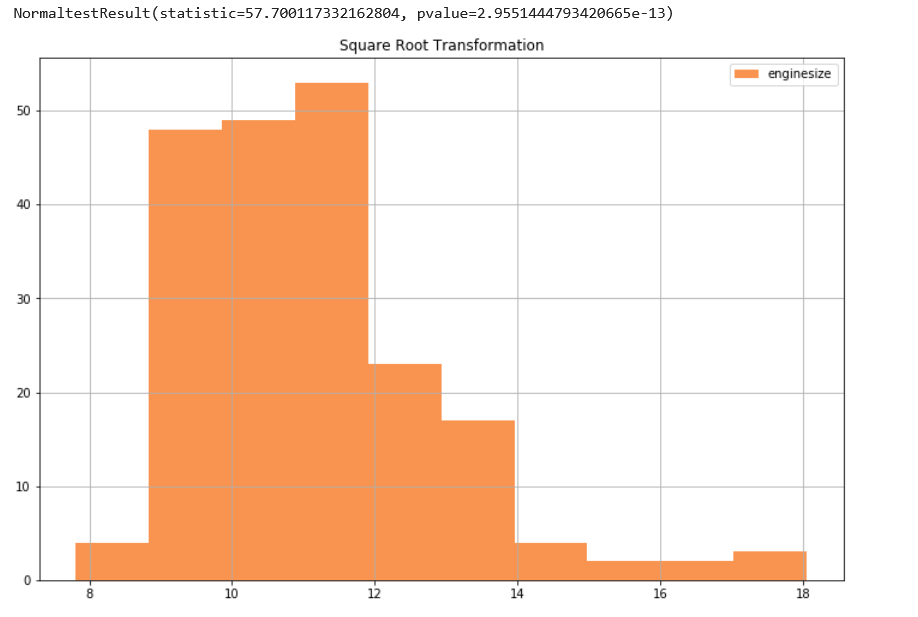
نلاحظ أن البيانات بعد التحويل باستخدام تحويل الجذر التربيعي قد تحسنت p-value = 2.95 x 10^-13 ولكن ليست بنفس درجة التحسين باستخدام التحويل اللوغاريتمي!

ثالثًا : التحويل بصندوق كوكس

يعتبر هذا التحويل من أفضل الأساليب المتبعة في هذا الصدد حيث يملك معامل Parameter من خلاله يتم الحصول على توزيعات “أقرب ما يمكن إلى التوزيع الطبيعي” فعن طريق تبديل القيمة لامبدا بشكل متكرر ومقارنة النتائج يمكننا الحصول على أفضل نتيجة ممكنة تناسب التوزيع المراد تحويله.

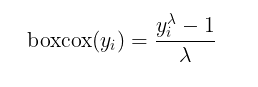
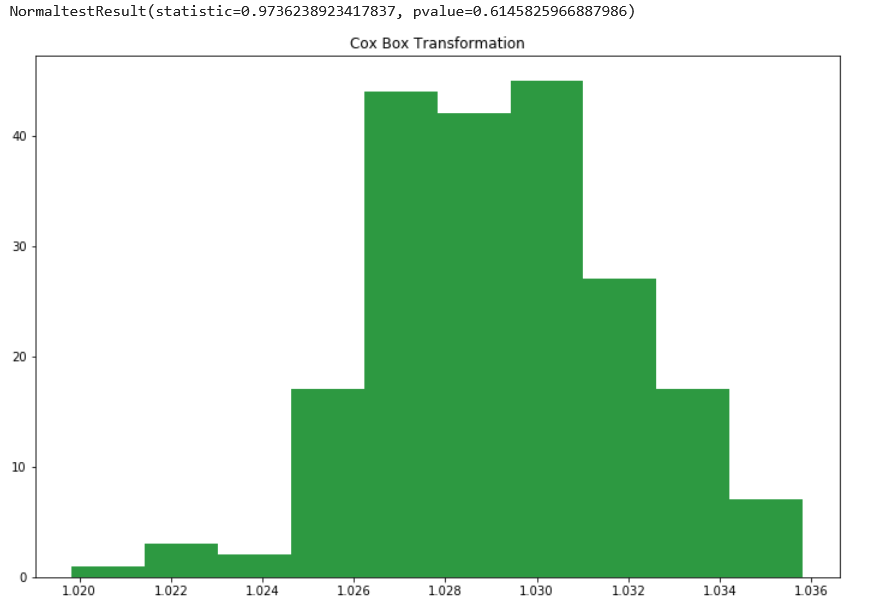
الآن كما نشاهد فقد حصلنا على أفضل نتيجة ممكنة من بين جميع الدوال السابقة حيث أن قيمة P تجاوزت العتبة التي وضعناها سابقًا بكثير p-value = 0.615 و أصبح الشكل مائلًا أكثر لكونه توزيعًا طبيعيًا.

مقارنة بين البيانات قبل التحويل وبعد التحويل من حيث كثافة وجود القيم المتطرفة:

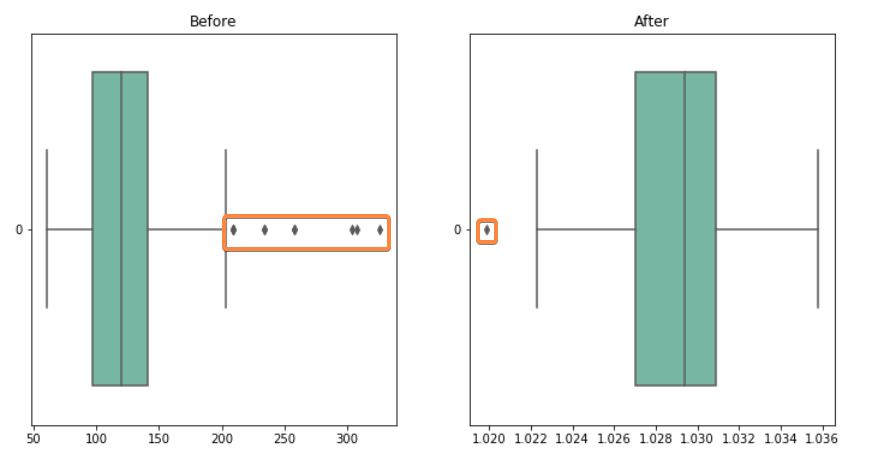
نلاحظ الفرق الكبير بين كثافة وجود القيم المتطرفة بين البيانات ماقبل تحويلها باستخدام صندوق كوكس وبعدها .

لن نتطرق في هذا الدرس إلى كيفية استخدام هذه البيانات المحولة في نماذج الانحدار فهي موضوع منفصل وقد يطول الدرس أكثر ولكن سنعمل على مقارنة بسيطة للعلاقة بين سعة المحرك وسعر السيارة لرؤية الفرق بين تبعثر البيانات قبل وبعد التحويل.

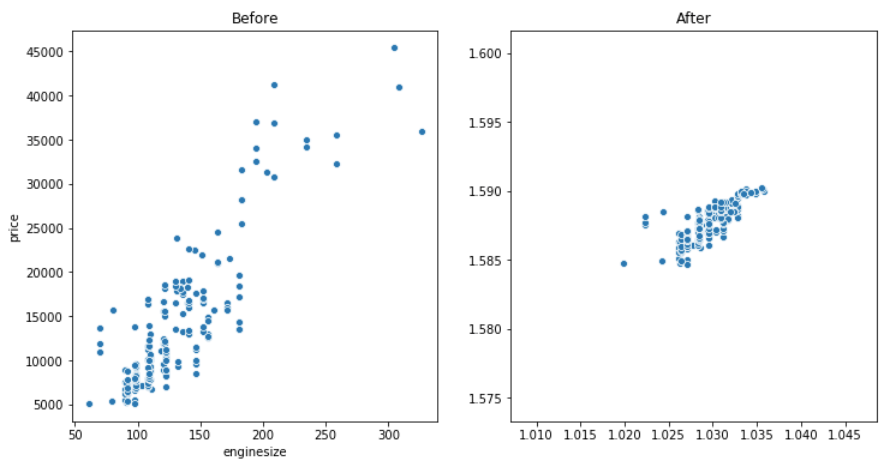
وبذلك ينتهي درسنا الذي أتمنى أن أكون قد وفقت في تقديمه بشكل مفهوم و مبسط.