تحليل البيانات الاستكشافي Exploratory Data Analysis (EDA) هو عملية فحص أو فهم البيانات واستخراج الأنماط والميزات الرئيسة والعلاقات المختلفة بينها وإيجاد القيم المتطرفة في البيانات وذلك لاستيعاب أفضل للمشكلة التي نريد حلها.

يعد تحليل البيانات الاستكشافي خطوة مهمة في أي مشروع يستخدم التعلم الآلي أو علم البيانات للإجابة عن أسئلة أو تقديم اقتراحات لصناعة القرار، حيث يتضمن هذا الأسلوب إنشاء إحصائيات موجزة للبيانات الرقمية وإنشاء تمثيلات رسومية مختلفة لفهم البيانات وذلك قبل الشروع في تطوير النماذج أو استخراج الأفكار النهائية (الاستبصارات) Insights بواسطة تلك البيانات.

سنتطرق في هذه المقدمة إلى نبذة مبسطة لأساسيات هذا الأسلوب وسنستخدم المكتبات الأشهر بلغة بايثون لفهم بيانات متعلقة بأداء مجموعة من الطلاب في الرياضيات، القراءة، والكتابة، تستند إلى تركيب سكاني وتحتوي على ميزات مختلفة مثل نوع الوجبة المعطاة للطالب، مستوى التحضير للاختبار، مستوى تعليم الوالدين، وغيرها، فمن خلال استخدام هذه البيانات يمكن حل أنواع مختلفة من مسائل الانحدار Regression والتصنيف Classification، كما يمكن استخدامها أيضًا لمعرفة العوامل التي يمكن أن تؤدي إلى درجات أفضل عمومًا في هذه الاختبارات.

بالإمكان تحميل كل من الـ Notebook و البيانات المستخدمة عبر النقر على الرابط 🔗 لتجربة الأكواد بنفسك:

1. استيراد المكتبات | Importing Libraries

2. سحب البيانات | Retrieving Data

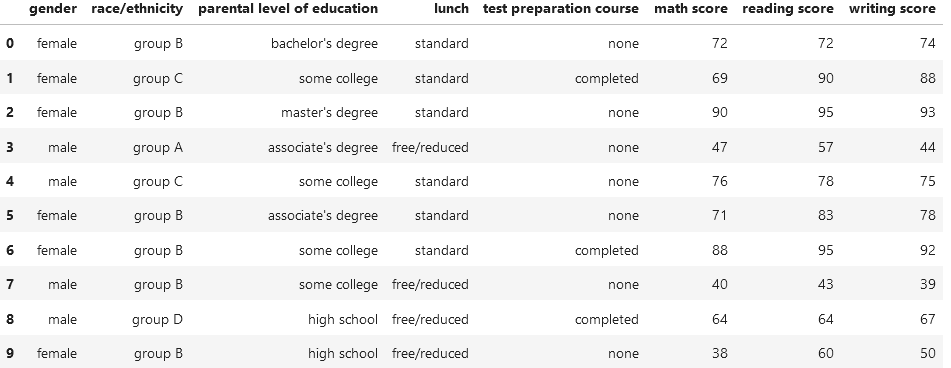
نلاحظ الآن وجود عدة أعمدة مكونة للبيانات التي نعمل عليها وهي مرتبة من اليسار إلى اليمين كالآتي:

• الجنس
• العرق / الإثنية
• المستوى التعليمي للوالدين
• وجبة الغداء المعطاة للطالب
• إكمال الدورة التحضيرية للاختبار
• نتيجة قسم الرياضيات
• نتيجة قسم القراءة
• نتيجة قسم الكتابة

كما نلاحظ وجود أسفل هذه الأعمدة بيانات رقمية numerical مثل نتائج الأقسام الثلاث للاختبار وأخرى فئوية Categorical مثل معلومات الجنس والعرق و المستوى التعليمي للوالدين.

أبعاد البيانات التي نعمل عليها:

تسمى الصفوف في مجموعة البيانات بالمشاهدات observations أو العينات samples بينما تسمى الأعمدة بالميزات أو الخصائص Features

عدد الصفوف في مجموعة البيانات : 1000

عدد الأعمدة في مجموعة البيانات : 8

3. الإحصاء الوصفي | Descriptive Statistics

في هذه الفقرة سنستخرج المعلومات الإحصائية للميزات (الأعمدة) عن طريق دالة describe المضمنة في مكتبة pandas وهذه المعلومات الإحصائية تشمل عدد العينات، المعدل، الانحراف المعياري، أقل و أكثر قيمة وغيرها.

أولاً: المعلومات الإحصائية الخاصة بالميزات الرقمية numerical features:

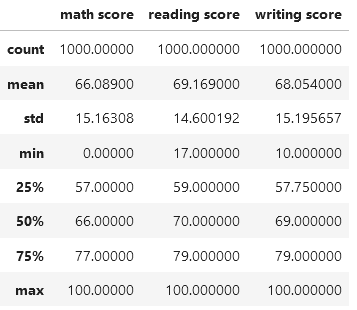
نلاحظ مايلي:

• عدد العينات count لكل من الأقسام الثلاثة للاختبار هو 1000
• المعدل mean : متقارب جدًا بين الأقسام الثلاث:
  • [الرياضيات : 66.09 ، القراءة : 69.17 ، الكتابة : 68.05]
• الإنحراف المعياري std : [الرياضيات : 15.19 ، القراءة : 14.60 ، الكتابة : 15.16]
• أقل قيمة min (أقل درجة في كل قسم) : [الرياضيات : 0.0 ، القراءة : 17.0 ، الكتابة : 10.0]
• الربع الأول First Quartile (25%) من الطلاب قد أحرزوا الدرجة التالية أو أقل في كل من :
  • [الرياضيات : 57.0 ، القراءة : 59.0 ، الكتابة : 57.0]
• الربع الثاني Second Quartile (25% – 50%) من الطلاب قد أحرزوا الدرجة التالية أو أقل في كل من :
  • [الرياضيات : 57.0 ، القراءة : 59.0 ، الكتابة : 57.0]

سنترك لك استنتاج كل من الربع الثالث و أكبر قيمة max بنفسك من خلال الجدول

ثانياً: بإمكانك استعراض المعلومات الإحصائية لكل من الميزات الرقمية والفئوية معًا :

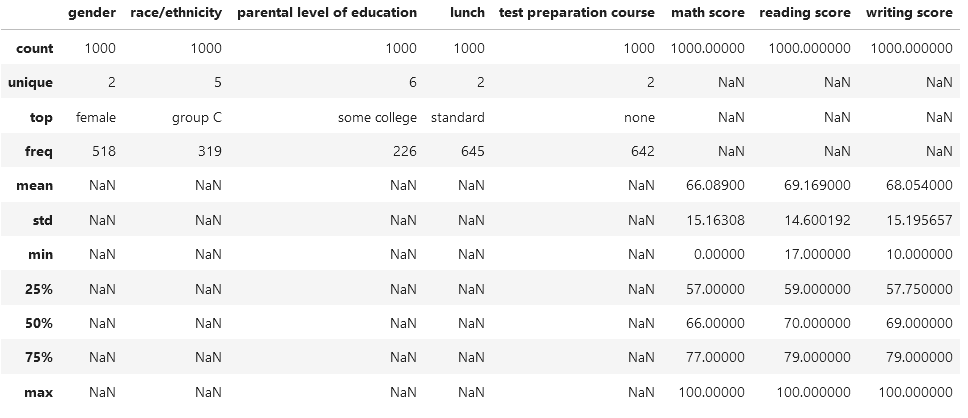
نلاحظ وجود معلومات احصائية جديدة كـعدد القيم الفريدة unique في كل ميزة و التسمية Label الأكثر وجودًا Top وعدد تكرارات تلك التسمية freq

مثال : ميزة المستوى التعليمي للوالدين تتضمن 6 تسميات أو قيم فريدة، والتسمية الأكثر وجودًا هي بعض الدراسة في كلية ‘some college’ حيث أنها تكررت 226 مرة في مجموعة البيانات.

ملاحظة: تشير القيمة NaN إلى عدم وجود قيمة إحصائية على سبيل المثال لا يمكن إيجاد أقل قيمة لميزة فئوية مثل العرق/الإثنية race/ethnicity

4. القيم المفقودة | Missing Values

يقصد بالقيم المفقودة القيم التي لا تحمل أي قيمة None على سبيل المثال لو أن أحد الطلاب رفض الإدلاء بنتيجة أحد أقسام الاختبار وليكن قسم الرياضيات فإن القيم المرتبطة بهذه الميزة وهذه العينة ستكون None

لحسن الحظ لا يوجد أي قيم مفقودة لدينا في أي من الميزات ولذلك لن نضطر إلى إجراء أي تعديلات بالوقت الراهن لتنظيف البيانات !

5. التحليل الرسومي | Graphical Analysis

في هذا الجزء ينبغي أن نتحلى بالفضول عن طريق طرح مجموعة من الأسئلة والفرضيات حول البيانات ولا داعي للقلق فهذه المهارة يتم اكتسابها مع الوقت والممارسة على مجموعات مختلفة من البيانات.

سنبدأ بالتحليل أحادي المتغير Univariate Analysis وسنستخدم الرسم البياني الشريطي Bar Graph لهذا الغرض. سننظر في توزيع الطلاب حسب الجنس والعرق / الإثنية وحالة الغداء وما إذا كان لديهم دورة تحضيرية للاختبار أم لا.

لنطرح السؤال التالي: ماهو عدد الطلاب الذين ارتادوا الاختبار من كلا الجنسين؟

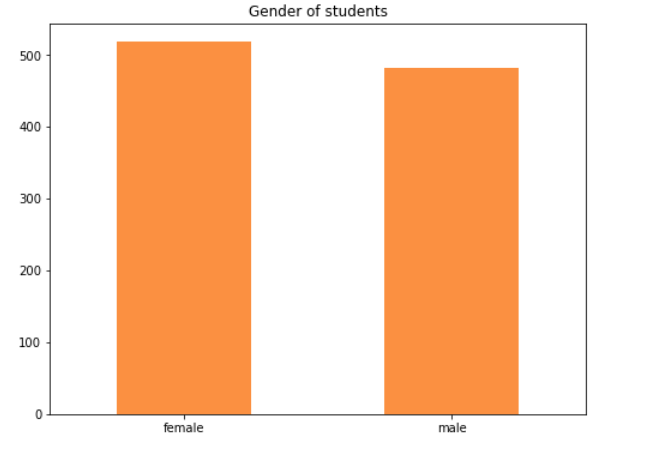
بالإمكان دمج عدة رسومات في واجهة واحدة حيث بإمكاننا الأجابة عن عدة أسئلة بنفس الوقت:

1- الرسم البياني الأول : مقارنة بين الطلاب المتمين و غير الحاصلين على دورة الاستعداد للاختبار

2- الرسم البياني الثاني: وصف لأنواع الوجبات التي تناولها الطلاب

3- الرسم البياني الثالث: مقارنة بين أعداد الطلاب وفقًا للعرق

4- الرسم البياني الرابع: مقارنة للمستوى التعليمي للوالدين

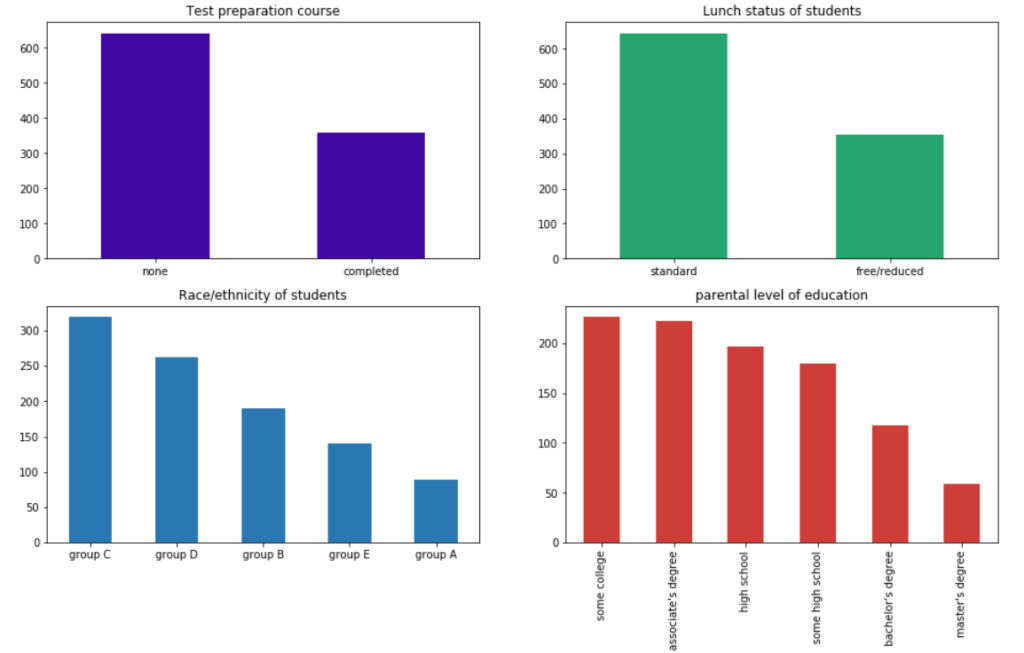
يمكن أن نلاحظ عدة أمور في الرسومات أعلاه على سبيل المثال ، عدد الطلاب الذين لم يأخذوا الدورة الاستعدادية للاختبار أكبر من الذين أخذوها بالضعف تقريبًا ، كما هو الحال مع وجبة الغداء القياسية التي سبقت الاختبار مقارنة بالذين لم يتناولوا أي شيء أو تناولوا القليل ، أيضًا نلاحظ أن أكثر عرقية تواجدًا في هذا الاختبار هي العرقية C و أقلها هي العرقية A ، بالإضافة إلى ذلك بإمكاننا استنتاج الحالة التعليمية للآباء.

تمثيل الصندوق | Box Plot Graph

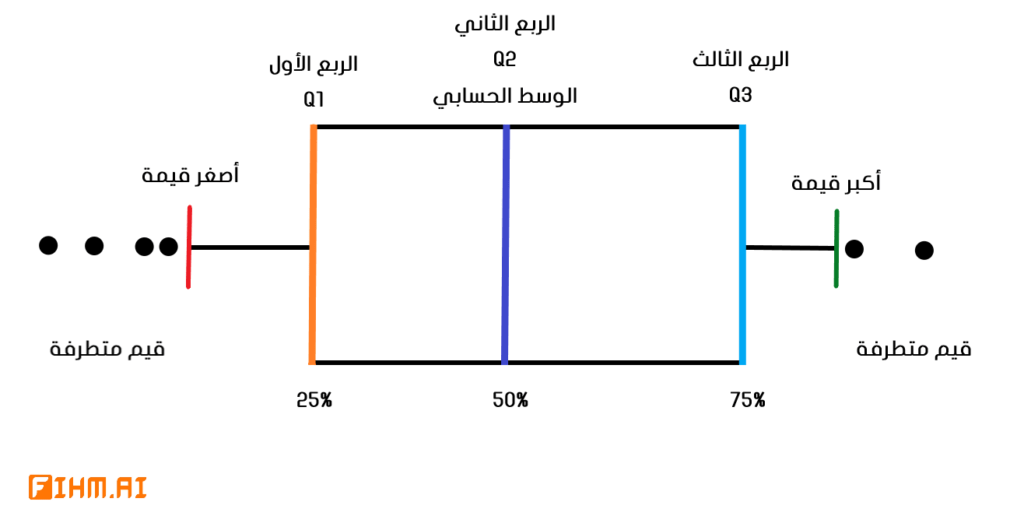
تمثيل الصندوق البياني Box Plot Graph وهو رسم يمكن من خلاله تحديد العديد من الأمور الإحصائية مثل نطاق الأرباع Quartiles الخاص بكل الميزات الرقمية و القيم المتطرفة، مانريد التركيز عليه الآن كيفية التعرف على وجود القيم المتطرفة في الرسم الصندوقي وهو أمر بغاية البساطة ، سنركز على أطراف الشكل فكل ماهو أكبر من أكبر قيمة Max أو أصغر من أصغر قيمة min سيٌّعد قيمة متطرفة ولو دققنا في الشكل أدناه لوجدنا أنه يوجد لدينا ست قيم متطرفة قيمتين أقصى الميمنة و أربع قيم أقصى الميسرة.

• 

الآن لنطبق الأمر عمليًا على مجموعة البيانات الخاصة بنا وتحديدًا الميزات الرقمية:

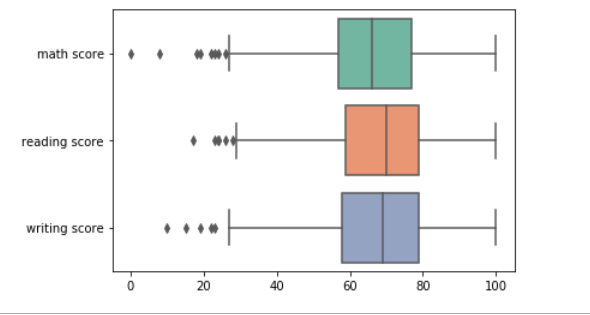
نشاهد بوضوع القيم المتطرفة لكل من أقسام الاختبار الثلاثة.

العلاقات بين الميزات | Features Correlations

الآن سندرس العلاقات بين الخصائص الرقمية وهي درجة قسم الرياضيات ، درجة قسم القراءة و درجة الكتابة

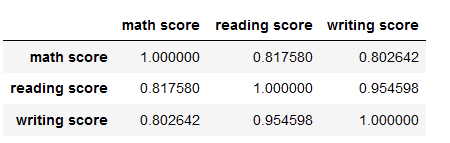
لقراءة العلاقات بين الميزات سنركز على الخلايا التي تنشأ من تقاطع كل عمود مع صف في الجدول باستثناء الخلايا التي تقع في قطر الجدول diagonal لأنها تعكس العلاقة بين الميزة ونفسها وهي بطبيعة الحال ستكون أقصى علاقة ممكنة 1.00000.

كلما كانت النتيجة قريبة من 1.0 فهذا يعني أن العلاقة الترابطية بين المتغيرات أو الميزات قوية وكلما اقتربت من 0.0 فهذا يعني ضعف العلاقة بين المتغيرات أو الميزات لنأخذ على سبيل المثال:

العلاقة بين درجة قسم الرياضيات و درجة قسم القراءة والتي تساوي 0.817580 حيث تعتبر علاقة قوية نسبياً ولكن لو قارن هذا بالعلاقة بين قسم الكتابة والقراءة سنجد أن العلاقة أقوى وتساوي 0.954598

خريطة الحرارة | Heat Map

هنالك رسم يسمى بخريطة الحرارة Heat Map سيسهل علينا قراءة الجدول السابق وخصوصاً في حال كنا تدرس العلاقة بين الكثير من الميزات في الوقت نفسه!.

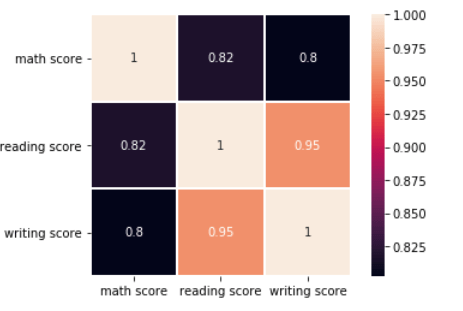
بنفس الطريقة سنقوم بتحييد القطر ونركز على بقية الخلايا ، حيث كلما أصبح لون الخلية مائلاً إلى الألوان الفاتحة كلما كانت العلاقة أقوى والعكس صحيح كلما كانت مائلة إلى ألوان أغمق كلما ضعفت العلاقة.

تمثيل النقاط المبعثرة | Scatter Points Plot

سنتحقق من العلاقة بين المزايا الرقمية ولكن هذه المرة من خلال تمثيل النقاط المبعثرة وسنحدد بالضبط فيما إذا كان العلاقة إيجابية أم سلبية ، طردية أم عكسية !

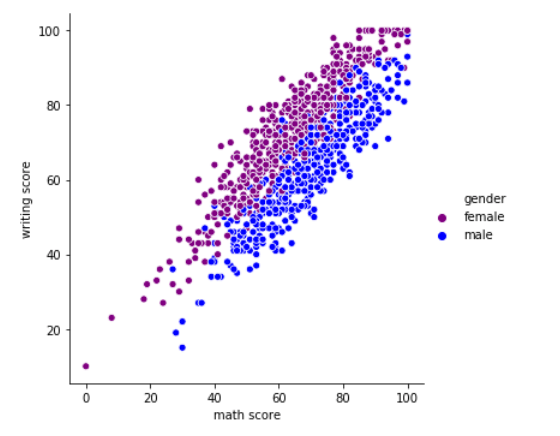
ما نلاحظه أن العلاقة طردية إيجابية أي أنه كلما كانت درجة قسم الرياضيات عالية فغالبًا ماستكون درجة قسم الكتابة عالية والعكس صحيح ما نلاحظه أيضًا أنه لايوجد فرق بين الجنسين في هذه العلاقة!

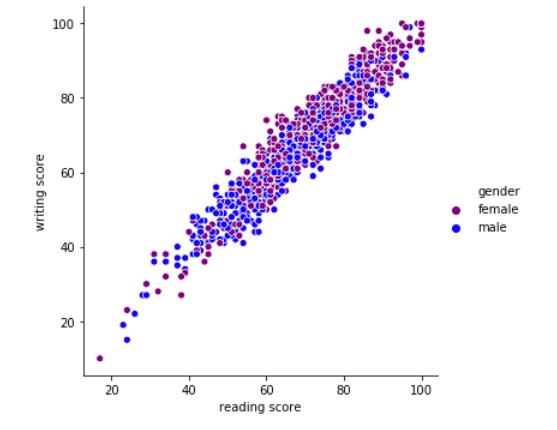
مانلاحظه هنا أيضًا أن العلاقة طردية و كلما كانت درجة قسم القراءة عالية فغالبًا ماستكون درجة قسم الكتابة عالية والعكس صحيح!

لنطرح سؤال آخر: هل يوجد علاقة بين المستوى التعليمي للآباء ودرجات الطلبة ؟

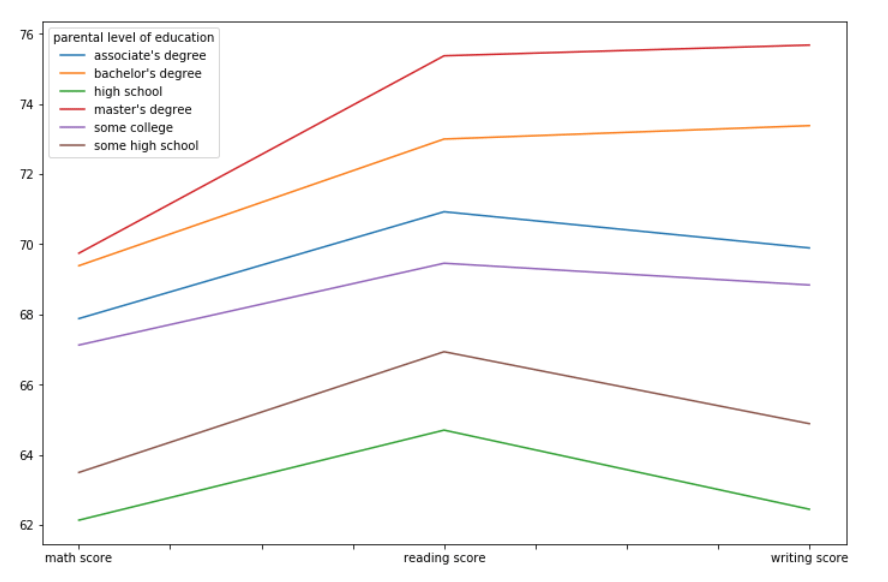
نلاحظ أنه كلما كان تعليم الوالدين أعلى كانت درجات أبناءهم أعلى وهذا مانلاحظه بالآباء الذين يحملون شهادة الماجستر و البكالوريوس في الرسم أعلاه ولكن هنالك مفارقة حيث أن درجات الطلاب الذين آبائهم لم يكملوا الثانوية العامة (اللون البني) هي أعلى من أولئك الذي أكملوها (اللون الأخضر)!

الآن لنضع فرضية كالآتي: درجة النجاح في قسم الرياضيات هي 60 درجة ولنختبر كم سينجح من الطلاب لو كانت هذه الفرضية مطبقة في هذه المدرسة !

677 من مجموع الطلاب تمكنوا من تجاوز قسم الرياضيات بينما 323 من مجموع الطلاب قد أخفقوا ، أي أن نسبة النجاح في هذا القسم هي 67.7 %

لنقوم بتمثيل ذلك من خلال المقارنة بين الجنسين !

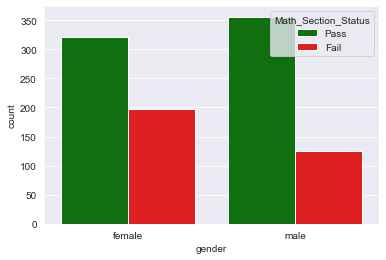
انتهى درسنا التقني ولم تنته الأساليب المتبعة في تحليل البيانات ولكن أتمنى أن أكون قد قدمت أسلوب تحليل البيانات الاستكشافي Exploratory Data Analysis بشكل سلس ومبسط للجميع ليتسنى للقارئ العربي فيما بعد الإبحار في هذا الأسلوب وتطبيقه في مشاريعه الخاصة في الذكاء الاصطناعي و علم البيانات !.