النزول أو الانحدار المتدرج (Gradient Descent) هي خوارزمية لإيجاد الحل الأمثل عن طريق تعديل قيمة المتغيرات للنموذج (model) للتقليل من قيمة دالة التكلفة في مرحلة تدريب النموذج وتستخدم في تدريب أنواع مختلفة من النماذج سواءً كانت في التعلم العميق أو غيره من أنواع تعلم الآلة.
خطوات عمل الخوارزمية
نبدأ بقيمة أولية للمتغير باختيار رقم عشوائيًا، وتسمى هذه العملية بالتهيئة العشوائية (Random Initialization)، ويوضح (الشكل 1) طريقة عمل الخوارزمية.
نقوم بتحسين قيمة المتغير وذلك عن طريق أخذ خطوات في اتجاه القيمة الصغرى العامة والتي تقلل قيمة دالة التكلفة، وتوضح الأشكال (2، 3، 4، 5) المعادلات.
نحسب حجم الخطوة وحجم الخطوة يعتمد على معامل سرعة التعلم مضروبًا في المَيْل، والميل يحسب من اشتقاق دالة التكلفة للمتغيرات.
نحسب القيمة الجديدة للمتغير عن طريق قيمة المتغير حاليا مطروحًا منها حجم الخطوة.
نكرر هذه العملية (
عدد مرات التكرار غالبا يكون رقم كبير لِتُعطى الخوارزمية وقتًا لإيجاد ، لكن عند ما تكون قيمة الانحدار المتدرج (GD) قيمة صغيرة، أي أصغر من قيمة التسامح (tolerance) ويرمز لها \epsilon وهي قيمة صغيرة جدا، تتوقف الخوارزمية لأنها تكون قد اقتربت جدا من .
أنواع خوارزمية الانحدار المتدرج
حزمة الانحدار المتدرج (Gradient Descent/Batch Gradient Descent): سميت بحزمة إلا أنها تتعامل مع كل البيانات الموجودة في كل دورة كحزمة من البيانات، وتكون بطيئةً جدا للوصول إلى القيمة الصغرى العامة إذا كانت البيانات كبيرة إلى حدٍ ما.
عشوائية الانحدار المتدرج (Stochastic Gradient Descent): يتم اختيار حالة واحدة فقط، وتنفذ العمليات الحسابية عليها، ويكون اختيار هذه الحالة عشوائيا، ولذلك سميت عشوائية الانحدار المتدرج، وتكون سريعة جدا ولا تواجه المشاكل إذا كانت البيانات كبيرة لأنها تتعامل في كل لحظة مع حالة واحدة فقط، إلا أنها تكون أقل انتظامًا من (BGD).
وتستخدم عشوائية الانحدار المتدرج جدول التعلم (Learning Schedule) حيث أن جدول التعلم يختار قيم معامل التعلم، ويبدأ بقيمة كبيرة وبعدها تبدأ قيمة المعامل بأن تصبح أصغر شيئا فشيئا إلى أن تصل الخوارزمية إلى القيمة الصغرى العامة، ويوضح (الشكل 6) نسبة الحالة للبيانات.
حزمة الانحدار المتدرج المصغرة (Mini-batch Gradient Descent): سميت بحزمة، وفي هذه الحالة المقصود بحزمة هنا جزء من البيانات في كل مرة، وليست كــحزمة الانحدار المتدرج التي تأخذ كل البيانات. وليست مثل عشوائية الانحدار المتدرج التي تأخذ حالة واحدة فقط، وتستخدم أيضا جدول التعلم لتحديد قيمة معامل التعلم، ويوضح (الشكل 7) مقارنة بين أنواع الخوارزمية.
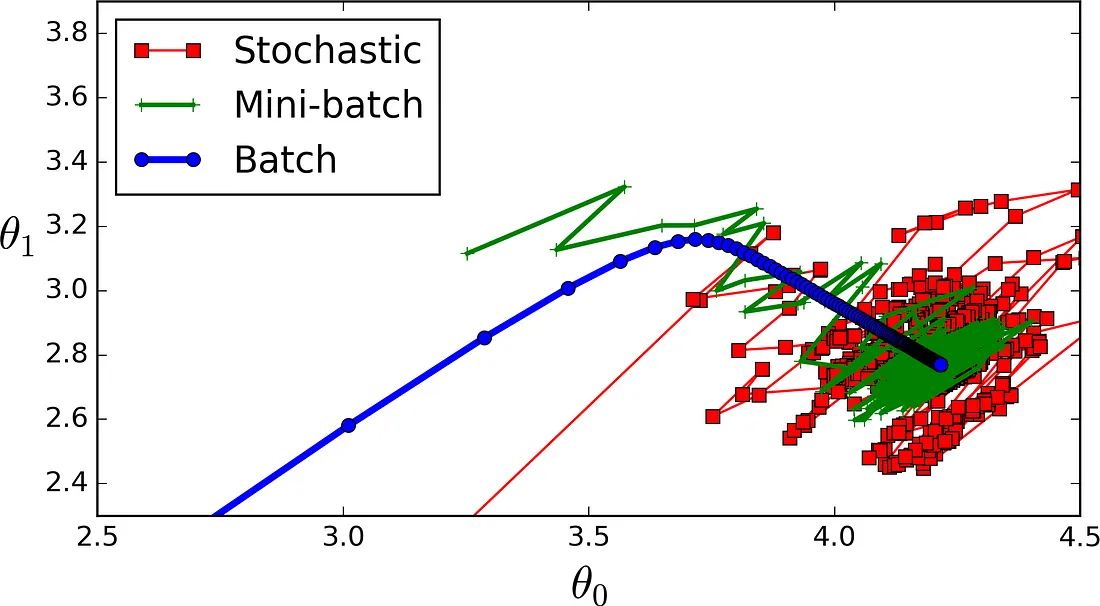
مقارنة بين أنواع الانحدار المتدرج
من العوامل التي تأثر على حساب الانحدار المتدرج (GD) إذا كان معامل سرعة التعلم صغيرًا جدًا يستوجب على الخوارزمية المرور بكثير من التكرارات إلى أن تصل إلى القيمة التي تجعل دالة التكلفة أقل ما يمكن، وتسمى هذه القيمة بــ .
أو إذا كان معامل سرعة التعلم كبيرًا جدًا فإن الخوارزمية تقفز من نقطة إلى أخرى، وهذا يعرضها لاحتمالية أنها قد تفشل للوصول إلى الحل الأمثل.
أما إذا كان معامل التعلم ثابتًا ستصل إلى الحل الأمثل في عدد من الخطوات تتمثل في \epsilon/1 واعتمادا أيضا على شكل دالة التكلفة، وتوصف هذه الحالة تحت مسمى (Convergence Rate).
التحديات
إذا كانت القيمة الابتدائية خطأ فهذا قد يقودنا إلى نتيجتين هما إما أن نصل إلى القيمة الصغرى المحلية أو نأخذ وقتًا طويلًا جدًا إلى أن نصل إلى القيمة الصغرى العامة.
اختفاء/انفجار قيمة التدرج (GD) في التعلم العميق، ويعود هذا إلى أن القيمة الابتدائية كانت صغيرة أو كبيرة، وعند اشتقاقات الدالة قد تصل إلى أن المَيْل يكون صفرًا أو رقما كبيرًا جدًا.
وفي الحالتين السابقتين يتم حلّهما نوعا ما عن طريق اختيار قيمة عشوائية كقيمة ابتدائية (التهيئة العشوائية).














