مقدمة
مرحبًا بكم مرة أخرى في سلسلة فهم لتعلم الآلة! في حديثنا السابق، تناولنا أساسيات التعلّم الغير خاضع للإشراف، حيث لا يتم تزويد نموذج تعلم الآلة بأي بيانات مصنّفة، وإنما يتم استخدام النموذج لرؤية الأنماط والعلاقات في البيانات. واليوم، سنواصل شرحنا حول التعلّم الغير خاضع للإشراف ونتعمق في تقنية شائعة تعرف باسم
إن التجميع هي تقنية تستخدم في التعلّم الغير خاضع للإشراف لتجميع نقاط البيانات المماثلة معًا. فهي تقوم بتقسيم مجموعة البيانات إلى مجموعات أو تجمعات بناءً على التشابه في الميزات. وتعتبر فوائد التجميع كثيرة، منها اكتشاف الأنماط المخفية في البيانات، وتحديد القيم الشاذة، وتبسيط مجموعات البيانات، والمساعدة في عمليات صنع القرار.
سنتعلم سويًا اليوم إحدى أهم التطبيقات لخوارزميات التجميع ألا وهي تقسيم العملاء، وهي عملية نقوم بها بتقسيم العملاء إلى مجموعات بناءً على الخصائص المشتركة مثل العمر والجنس والاهتمامات وعادات الشراء وغيرها. من خلال تجميع العملاء في مجموعات بناءً على التشابهات بينهم، يمكن للشركات إنشاء حملات تسويق مستهدفة، وتخصيص المنتجات والخدمات لمجموعات العملاء المحددة، وتحسين رضا العملاء. يعتبر التجميع فعالًا في تقسيم العملاء لأنه يساعد في تحديد مجموعات من العملاء ذوي التفضيلات والسلوكيات المشابهة، مما يسمح للشركات بتخصيص نهجها وزيادة المبيعات.
ماذا نريد أن نفعل؟
في درس اليوم، سوف نحاول الحصول على أنماط سلوك العملاء للوصول إلى استنتاجات مفيدة، ولذلك فإنه من المهم تحليل البيانات وتحديد الأنماط المحتملة التي قد تكون مخفية. في البداية سوف نقوم بذلك من خلال رسم البيانات بشكل عام، والتي تسمح لنا باستكشاف وفهم البيانات بسرعة وتحديد أين تتجمع البيانات والاتجاهات والقيم الشاذة. وبعد أن نقوم بفهم البيانات بشكل أفضل، سوف نقوم بتطبيق خوارزمية التجميع لتجميع نقاط البيانات المشابهة معًا.
إن قيامنا باستخدام خوارزميات التجميع بعد رسم البيانات سوف يساعدنا في تحديد الأنماط والتشابهات في البيانات التي قد لا تكون واضحة على الفور. والتي سوف تساعدنا في فهم علاقات المتغيرات المختلفة وتحديد العوامل الرئيسية التي قد تحدد سلوك العملاء.
البيانات المستخدمة في هذا الدرس
في هذا الدرس سوف نستخدم بيانات العملاء لمجمع تجاري من أجل دراسة أنماط العملاء والعوامل المشتركة بينهم
ويمكنكم الاطلاع على البيانات من مصدرها الأساسي عن طريق الرابط التالي
خوارزمية التجميع المستخدمة في هذا الدرس
في تحليلنا، سنستخدم خوارزمية تجميع تسمى وهي خوارزمية تستخدم لتجميع نقاط البيانات المتشابهة معًا بناءً على بعدهم عن بعضهم البعض. يمثل حرف الـ عدد المجموعات التي سوف يتم تقسييم العملاء إليها، وسوف نتناول في درس اليوم كيفية اختيار العدد المناسب من المجموعات.
الخطوة الأولى: استكشاف البيانات
كالعادة، خطوتنا الأولى هي استكشاف البيانات الوصفية للبيانات من أجل التحقق من جودة البيانات المستخدمة وأخذ نظرة شاملة عن البيانات
# Reading data
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/KAFSALAH/Fihm_Lessons/master/ML_Series6_Clustering/Mall_Customers.csv')
print('Data first five rows are')
display(df.head())
print('Data dimensions are')
display(df.shape)
print('Data types are')
display(df.dtypes)
print('Is there missing values?')
display(df.isnull().values.any())
| CustomerID | Gender | Age | Annual Income (k$) | Spending Score (1-100) | |
|---|---|---|---|---|---|
| 0 | 1 | Male | 19 | 15 | 39 |
| 1 | 2 | Male | 21 | 15 | 81 |
| 2 | 3 | Female | 20 | 16 | 6 |
| 3 | 4 | Female | 23 | 16 | 77 |
| 4 | 5 | Female | 31 | 17 | 40 |
إن الميزة الأولى
إن أهمية المفتاح الأساسي تكمن في تسهيل عملية تخزين بيانات العملاء في قواعد البيانات، والآن وبعد أن تم سحب البيانات من قاعدة البيانات، نقوم بإزالة العمود لأن ليس له معنى رياضيْ ذو قيمة، أي أن العميل الذي رقم معرفه 50 لا يعني بالضرورة أنه ينفق أكثر من العميل رقم معرفه 49.
df.drop('CustomerID', axis = 1, inplace = True)
الخطوة الثانية: رسم البيانات عن طريق تحليل متغير واحد
نستهل عملية تحليل بيانات العملاء برسم كل متغير على حدة و من ثم رؤية كيفية توزيع قيم المتغير
توزيع نسب الذكور والإناث
import matplotlib.pyplot as plt
plt.style.use('bmh')
plt.figure(figsize = (6 , 4))
counts = df['Gender'].value_counts() # We count number of males and females
ax = counts.plot(kind='bar', color = ['teal','darkred'])
# add text labels to the top of the bars
for i, count in enumerate(counts):
ax.text(i, count+1, str(count), ha='center')
plt.title('Customers Genders')
plt.xticks(rotation=0)
plt.ylabel('Counts')
plt.show()
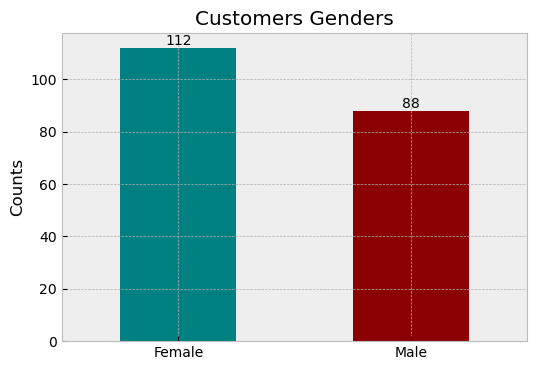
نسبة العملاء النساء أكثر من الرجال. حيث أن النساء يمثلون 56% بينما الرجال يمثلون 44% من العملاء.
توزيع العمر، الدخل، ودرجة الإنفاق
import warnings
warnings.filterwarnings("ignore") # Muting ditsplot warnings
import seaborn as sns
plt.figure(figsize = (18, 6))
i = 0
for x in ['Age' , 'Annual Income (k$)' , 'Spending Score (1-100)']:
i += 1
plt.subplot(1 , 3 , i)
plt.subplots_adjust(hspace =0.5 , wspace = 0.5)
sns.distplot(df[x], bins=20)
plt.title('{} Distribution Plot'.format(x))
plt.show()
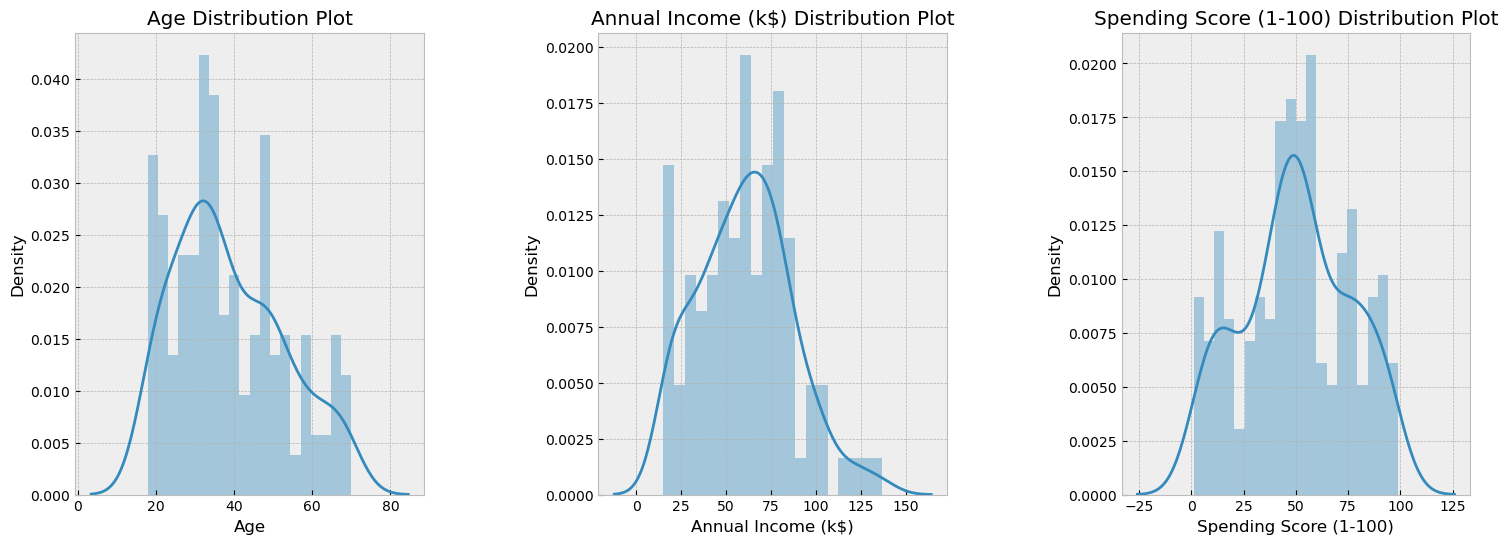
تتراوح أعمار العملاء ما بين العشرون إلى السبعون. بينما يتراوح دخل الأغلبية ما بين 35 إلى 85 ألفا. وأخيرًا، نلاحظ أن درجة إنفاق العملاء متوزعة توزيعًا طبيعيًا أي أن الأغلبية لديهم درجة إنفاق مساوية للمتوسط ألا وهي الـــ 50.
إن رسمنا لكل متغير على حدة يساعدنا في أخذ صورة عامة عن العملاء وكيفية توزيع بياناتهم. الخطوة التالية هي استكشاف العلاقة بين المتغيرات باستخدام التحليل ثنائي المتغيرات.
الخطوة الثالثة: رسم البيانات عن طريق تحليل متغيرين سويًا
الأن، سوف نقوم بتحليل العلاقة بين متغيرين سويًا باستخدام رسمة تعرف بــ Scatter Plot التي يتم فيها تمثيل كل عميل بنقطة واحدة لرؤية نمط العلاقة بين المتغيرات.
علاقة العمر بالدخل السنوي
# Age Vs Annual Income
plt.figure(figsize = (15 , 6)) # Figure size
for gender in ['Male','Female']: # Legends
plt.scatter(x = 'Age' , y = 'Annual Income (k$)' , data = df[df['Gender'] == gender],
s = 150 , alpha = 0.6 , label = gender)
plt.xlabel('Age'), plt.ylabel('Annual Income (k$)')
plt.title('Age vs Annual Income')
plt.legend()
plt.show()
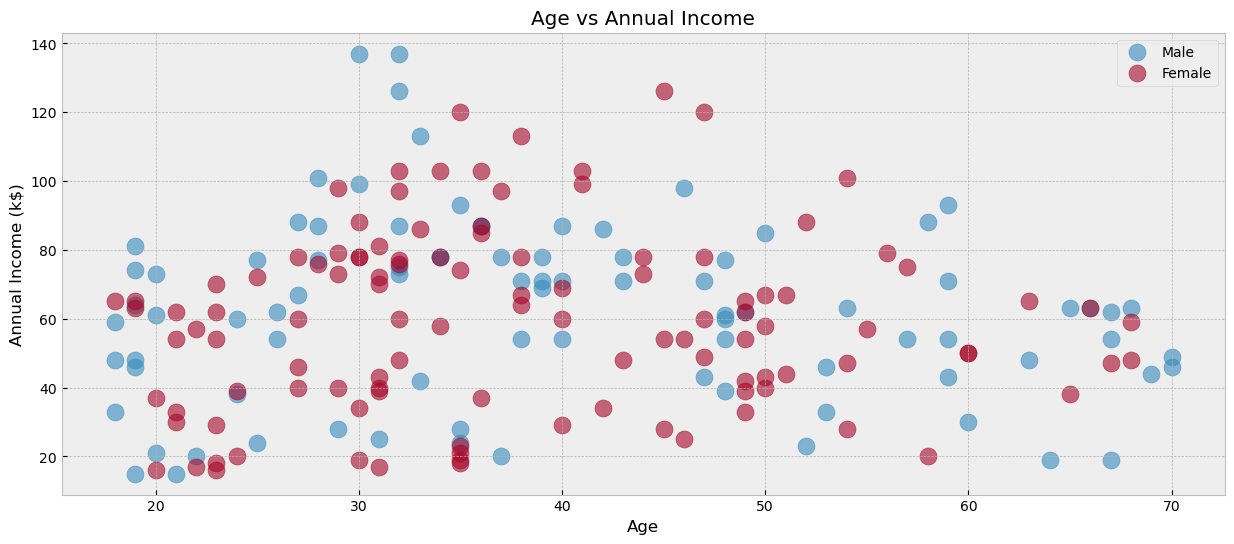
قمنا برسم العلاقة ما بين العمر والدخل السنوي. نلاحظ أن أغلب العملاء الذين يتجاوز دخلهم الـ100 ألف تتراوح أعمارهم ما بين الـ28 إلى 48 سنة. قمنا أيضا بتلوين النقاط بناء على جنس العميل مما يجعلنا نرى علاقة الجنس أيضا على الدخل السنوي. سنقوم الآن باستكشاف العلاقات الأخرى وتطبيق خوارزمية التجميع لرؤية كيفية استخدامها في فهم سلوك العملاء.
علاقة العمر بدرجة الإنفاق
plt.figure(figsize = (15 , 6))
for gender in ['Male','Female']:
plt.scatter(x = 'Age' , y = 'Spending Score (1-100)' , data = df[df['Gender'] == gender] ,
s = 150 , alpha = 0.6 , label = gender)
plt.xlabel('Age'), plt.ylabel('Spending Score (1-100)')
plt.title('Age vs Spending Score')
plt.legend()
plt.show()
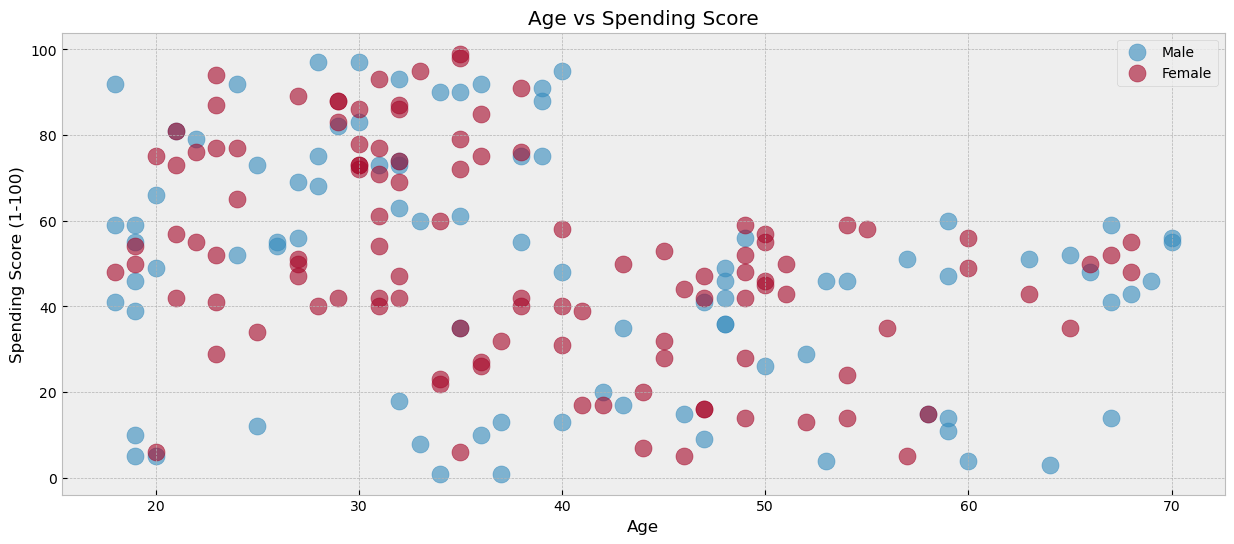
بدأت الآن تظهر لنا بعض الأنماط الواضحة للعملاء. فمثلًا، نلاحظ أن العملاء الأكبر من 40 سنة لا يتجاوز معدل إنفاقهم الـ60 نقطة. ومن الناحية الأخرى فإنه من النادر رؤية عميل أقل من الـ30 سنة لديه معدل إنفاق أقل من الـ40 نقطة. من هنا نبدأ نستنتج أن هناك مجموعات مختلفة من العملاء، وأنه يوجد لكل مجموعة ديموغرافية وأنماط سلوكية معينة في الشراء. إن فهمنا لهذه الأنماط وتحديد المجموعات بشكل صحيح سيسهم بشكل فعال في زيادة الأرباح من خلال ما يعرف بالإعلانات المخصصة.
فلنقم الآن بتطبيق خوارزمية K-Means من أجل تقسيم العملاء بناء على ميزتي العمر ودرجة الإنفاق إلى مجموعات مصغرة، ومن الجدير بالذكر أنه لا بدَّ من اختيار كم عدد المجموعات الذي نريد تقسيم البيانات إليها. مبدئيًا سوف نختار الآن أن يتم تقسيم العملاء إلى أربع مجموعات، وسوف نتحدث لاحقًا عن كيفية اختيار عدد المجموعات المناسب.
Age_Spending = df[['Age','Spending Score (1-100)']].iloc[: , :].values # Taking only age and spending score columns
from sklearn.cluster import KMeans
algorithm = KMeans(n_clusters = 4) # Initializing K-means algorithm using 4 clusters.
algorithm.fit(Age_Spending)
labels1 = algorithm.labels_
centroids1 = algorithm.cluster_centers_
معلومات النموذج
تمثيل النموذج بشكل بصري لرؤية المجموعات الناتجة بناء على العمر والإنفاق
import numpy as np
h = 0.02
x_min, x_max = Age_Spending[:, 0].min() - 1, Age_Spending[:, 0].max() + 1
y_min, y_max = Age_Spending[:, 1].min() - 1, Age_Spending[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
plt.figure(figsize = (15 , 7))
plt.clf()
Z = Z.reshape(xx.shape)
plt.imshow(Z , interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
cmap = plt.cm.Pastel2, aspect = 'auto', origin='lower')
plt.scatter( x = 'Age' ,y = 'Spending Score (1-100)' , data = df , c = labels1 ,
s = 200 )
plt.scatter(x = centroids1[: , 0] , y = centroids1[: , 1] , s = 300 , c = 'red' , alpha = 0.5)
plt.ylabel('Spending Score (1-100)') , plt.xlabel('Age')
plt.show()
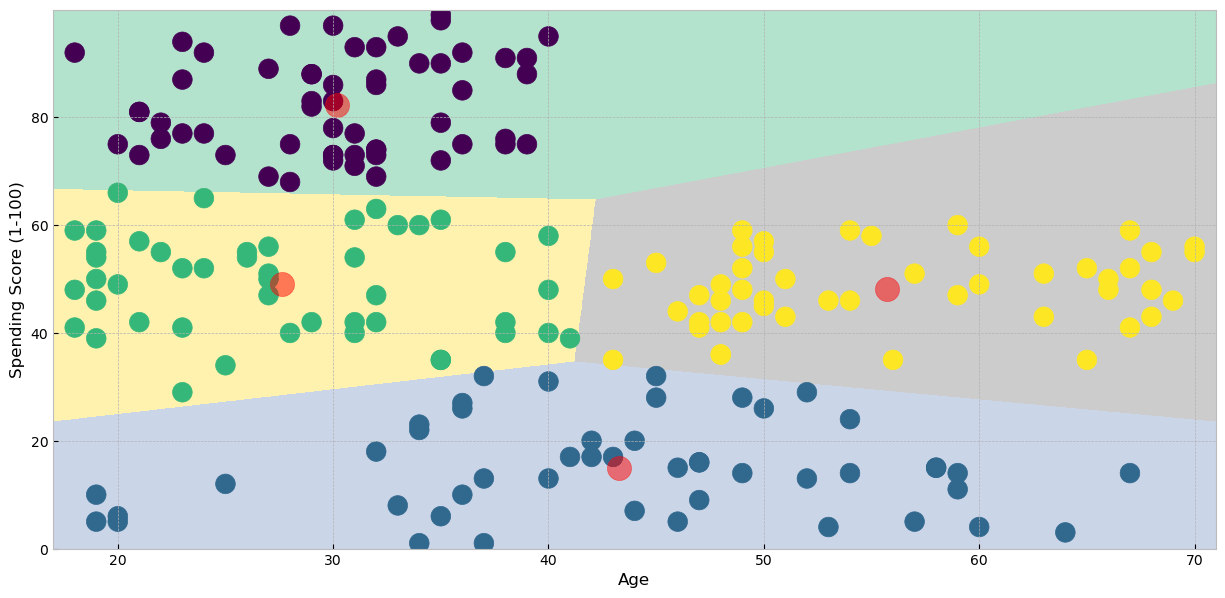
قمنا بتقسيم العملاء إلى أربع مجموعات والنمط الغالب في المجموعات كما يلي:
من الجدير بالذكر أيضًا أن نقطة المنتصف لكل مجموعة Cluster Centriod وهو معيار مهم لتحديد المجموعة التي تنتمي لها نقطة معينة بناء على المسافة بينها وبين نقطة المنتصف.
علاقة الدخل السنوي بدرجة الإنفاق
plt.figure(figsize = (15 , 6))
for gender in ['Male','Female']:
plt.scatter(x = 'Annual Income (k$)' , y = 'Spending Score (1-100)' , data = df[df['Gender'] == gender] ,
s = 150 , alpha = 0.6 , label = gender)
plt.xlabel('Annual Income (k$)'), plt.ylabel('Spending Score (1-100)')
plt.title('Annual Income (k$) vs Spending Score')
plt.legend()
plt.show()
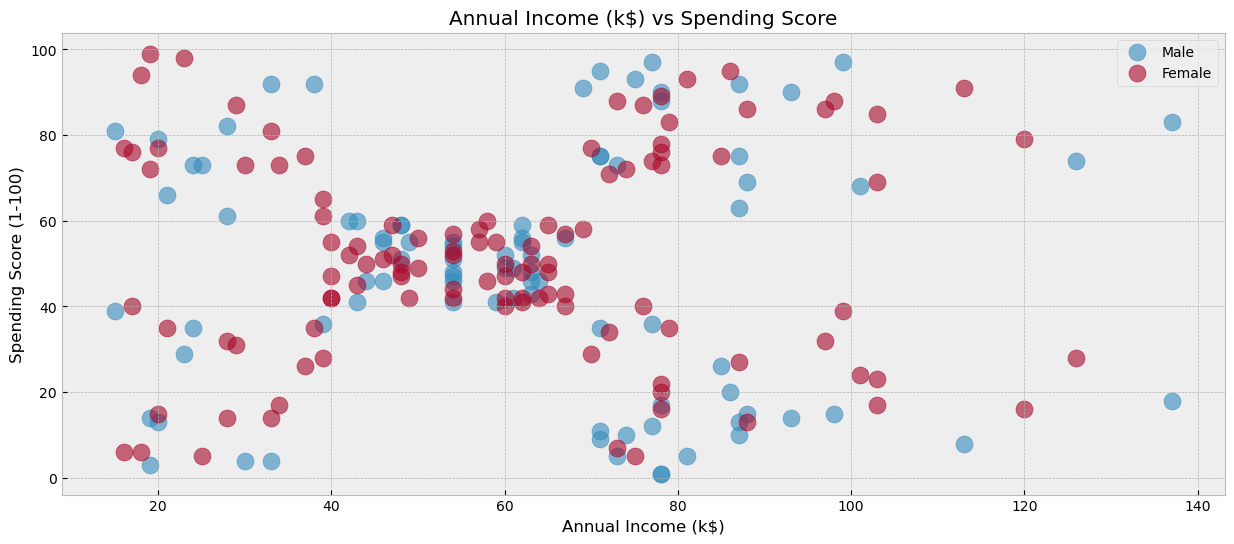
نلاحظ هنا أيضًا أنماطًا واضحة. على سبيل المثال، نستطيع بسهولة رؤية أن هناك خمس مجموعات للعملاء. إحدى هذه المجموعات هي مجموعة العملاء الذين تتراوح نقاط الإنفاق لديهم ما بين الــ 40 و 60. فلنقم الآن بتطبيق خوارزمية التقسيم كما يلي
Income_Spending = df[['Annual Income (k$)' , 'Spending Score (1-100)']].iloc[: , :].values
algorithm = KMeans(n_clusters = 5) # Initializing K-means algorithm using 5 clusters.
algorithm.fit(Income_Spending)
labels2 = algorithm.labels_
centroids2 = algorithm.cluster_centers_
معلومات النموذج
تمثيل النموذج بشكل بصري لرؤية المجموعات الناتجة بناء على الدخل السنوي والإنفاق
h = 0.02
x_min, x_max = Income_Spending[:, 0].min() - 1, Income_Spending[:, 0].max() + 1
y_min, y_max = Income_Spending[:, 1].min() - 1, Income_Spending[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z2 = algorithm.predict(np.c_[xx.ravel(), yy.ravel()])
plt.figure(figsize = (15 , 7))
plt.clf()
Z2 = Z2.reshape(xx.shape)
plt.imshow(Z2 , interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
cmap = plt.cm.Pastel2, aspect = 'auto', origin='lower')
plt.scatter( x = 'Annual Income (k$)' ,y = 'Spending Score (1-100)' , data = df , c = labels2 ,
s = 200 )
plt.scatter(x = centroids2[: , 0] , y = centroids2[: , 1] , s = 300 , c = 'red' , alpha = 0.5)
plt.ylabel('Spending Score (1-100)') , plt.xlabel('Annual Income (k$)')
plt.show()
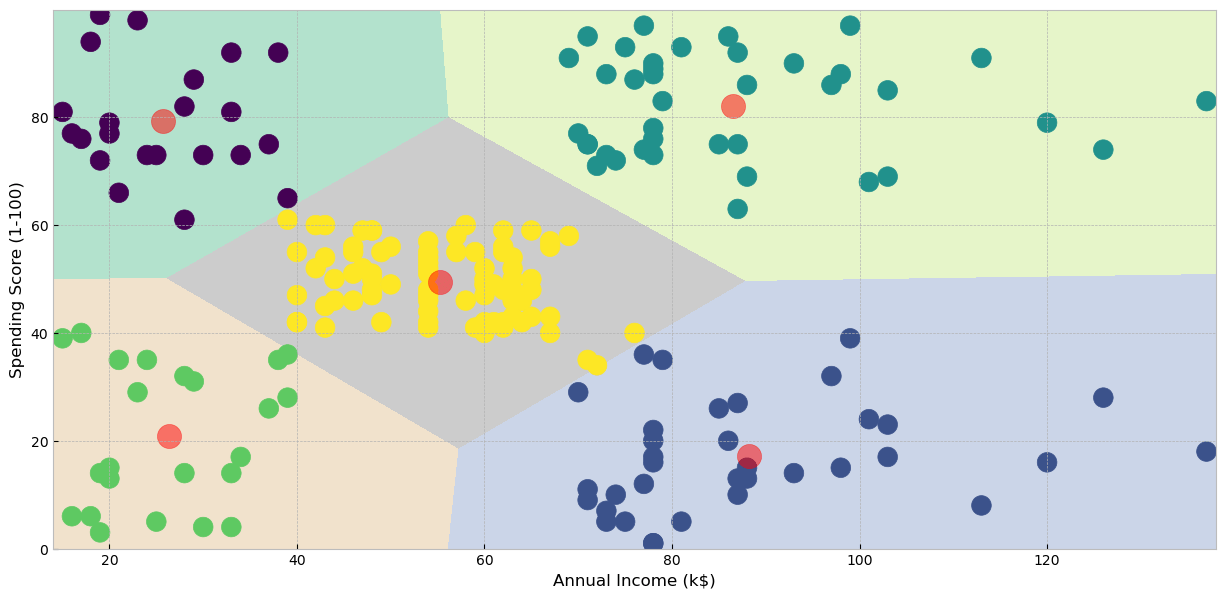
قمنا بتقسيم العملاء إلى خمس مجموعات والنمط الغالب في المجموعات كما يلي:
الخطوة الرابعة: رسم البيانات عن طريق تحليل ثلاثة متغيرات سويًا
سنقوم الآن بأخذ العمر، الدخل السنوي، ومعدل الإنفاق سويًا ورؤية المجموعات الناتجة
df_backup = df.copy() # Taking a back up of data for later use
df.drop('Gender',axis = 1, inplace = True) # Removing gender columns
df_columns = df.columns.to_list()
df_columns # The used columns are
df.head()
| Age | Annual Income (k$) | Spending Score (1-100) | |
|---|---|---|---|
| 0 | 19 | 15 | 39 |
| 1 | 21 | 15 | 81 |
| 2 | 20 | 16 | 6 |
| 3 | 23 | 16 | 77 |
| 4 | 31 | 17 | 40 |
إعادة وزن البيانات Min-Max Scaling
سنقوم الأن بتطبيق أمرٍ مهم لم نقم بصنعه بالخطوات الماضية ألا وهو إعادة وزن قيم البيانات باستخدام Min-max Scaling وذلك من أجل جعل مجال القيم في كل عمود يتراوح ما بين الصفر والواحد من أجل ضمان أن كل عمود له أثر مساوي في تحديد قيمة المنتصف لكل مجموعة. لإنه إن لم نقم بإعادة وزن الأعمدة وكان لدينا عمود ذو قيمة عالية، سوف يكون معظم تركيز النموذج عليه فقط دون غيره من الأعمدة. لحسن الحظ أن مجال الأعمدة المستخدمة في بيانات اليوم متقاربة من بعضها لبعض، ولذلك أمكننا عمل تقسيم للمجموعات بدون تطبيق في الأمثلة السابقة. ولكن الأولى دائما هو إعادة وزن البيانات Unified Scaling من أجل ضمان عدم انحيازية النموذج.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
df[df_columns] = scaler.fit_transform(df[df_columns])
df.head()
| Age | Annual Income (k$) | Spending Score (1-100) | |
|---|---|---|---|
| 0 | 19 | 15 | 39 |
| 1 | 21 | 15 | 81 |
| 2 | 20 | 16 | 6 |
| 3 | 23 | 16 | 77 |
| 4 | 31 | 17 | 40 |
اختيار العدد الأمثل من المجموعات
حسنًا، نريد الآن أن نختار عدد المجموعات المناسب الذي سوف نقوم بتقسيم العملاء عليه. إن قمنا باختيار عدد مجموعات قليل (مجموعتين مثلًا) فلن نستطيع الحصول على أنماط مميزة لكل مجموعة، وإن قمنا باختيار عدد كبير جدًا مثل عشر مجموعات، فسيكون لدنيا أنماطٌ محددة جدًا ومن المكلف دراسة كل نمط على حدة. ولذلك نريد أن نصل إلى عدد معين لتدريب النموذج بشكل مناسب مع اجتناب تشبع النموذج، وللقيام بذلك سوف نقوم بتعريف مصطلحين مهمين ألا وهم القصور الذاتي وطريقة الكوع.
القصور الذاتي هو مقياس لمدى انتشار المجموعات. يتم حسابه عن طريق تلخيص المسافات المربعة بين كل نقطة في الكتلة والنقطة الوسطى لتلك المجموعة. يُستخدم القصور الذاتي كمعيار لتقييم جودة خوارزمية التجميع. حيث أن هدفنا هنا هو تقليل القصور الذاتي إلى حد مقبول ولا نريد تقصيره إلى صفر لتجنب تشبع النموذج.
طريقة الكوع هي تقنية رسومية تُستخدم لتحديد العدد الأمثل للمجموعات في مجموعة البيانات عن طريق رسم القصور الذاتي للمجموعات بناء على عدد المجموعات المستخدم. ستُظهر الرسمة عادةً نقصًا في القصور الذاتي مع زيادة عدد المجموعات. ومع ذلك، في مرحلة ما، سيبدأ معدل الانخفاض في الاستقرار، مما يخلق انحناءً في الرسمة يشبه الكوع. غالبًا ما يُعتبر عدد المجموعات في هذه المرحلة هو العدد الأمثل للمجموعات.
باستخدام طريقة الكوع يمكننا تحديد العدد الأمثل المجموعات الذي يوازن بين تعقيد النموذج وجودة التدريب. إذا حددنا عددًا قليلاً جدًا من المجموعات، فقد نفقد أنماطًا مهمة في البيانات. من ناحية أخرى، إذا حددنا عددًا كبيرًا جدًا من المجموعات، فقد نقوم بإفراط في تجميع البيانات وإنشاء مجموعات صغيرة جدًا أو محددة جدًا بحيث لا تكون مفيدة
القيام بتجربة أعداد مختلفة من المجموعات
سنقوم الآن بتجربة تقسيم البيانات إلى مجموعتين، ثم ثلاثة، وهكذا وصولا إلى عشر مجموعات. ومن ثم سنختار عدد المجموعات المناسب
# Create and fit a range of models
km_list = list()
for clust in range(1,11): # Test 10 clusters
km = KMeans(n_clusters = clust, random_state=123) # Initiate the model
km = km.fit(df[df_columns])
km_list.append(pd.Series({'clusters': clust,
'inertia': km.inertia_,
'model': km}))
# Inertia elbow
plot_data = (pd.concat(km_list, axis=1)
.T
[['clusters','inertia']]
.set_index('clusters'))
ax = plot_data.plot(marker='o',ls='-')
ax.set_xticks(range(0,11,1))
ax.set_xlim(0,11)
ax.set(xlabel='Cluster', ylabel='Inertia');
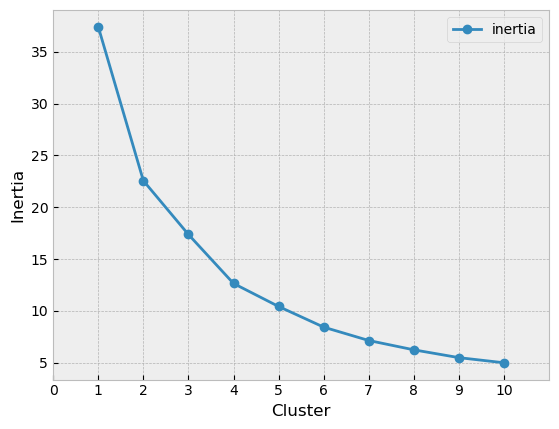
نلاحظ أن القصور الذاتي يقل مع زيادة عدد المجموعات. ولكن كمية النزول بعد العدد 4 تبدأ في التضاؤل وتصبح طفيفة. لذلك سنقوم باختيار 4 كعدد المجموعات الذي نريد تقسيم البيانات عليه
algorithm = (KMeans(n_clusters = 4 ,init='k-means++', n_init = 10 ,max_iter=300,
tol=0.0001, random_state= 111 , algorithm='elkan'))
algorithm.fit(df)
labels3 = algorithm.labels_
centroids3 = algorithm.cluster_centers_
خطوة إضافية: استخدام عمود الجنس في عملية التجميع
إذا أردنا استخدام ميزة الجنس في عملية تقسيم المجموعات. فلابد من إجراء عملية الترميز لتحويل بيانات الجنس إلى أرقام كالتالي
df = pd.get_dummies(df_backup)
df_columns = df.columns.tolist()
display(df.head())
display(df_columns)
| Age | Annual Income (k$) | Spending Score (1-100) | Gender_Female | Gender_Male | |
|---|---|---|---|---|---|
| 0 | 19 | 15 | 39 | 0 | 1 |
| 1 | 21 | 15 | 81 | 0 | 1 |
| 2 | 20 | 16 | 6 | 1 | 0 |
| 3 | 23 | 16 | 77 | 1 | 0 |
| 4 | 31 | 17 | 40 | 1 | 0 |
'Annual Income (k$)',
'Spending Score (1-100)',
'Gender_Female',
'Gender_Male']
ومن ثم نقوم بإعادة وزن الأعمدة كما قمنا بالسابق
scaler = MinMaxScaler()
df[df_columns] = scaler.fit_transform(df[df_columns])
df
| Age | Annual Income (k$) | Spending Score (1-100) | Gender_Female | Gender_Male | |
|---|---|---|---|---|---|
| 0 | 0.019231 | 0.000000 | 0.387755 | 0.0 | 1.0 |
| 1 | 0.057692 | 0.000000 | 0.816327 | 0.0 | 1.0 |
| 2 | 0.038462 | 0.008197 | 0.051020 | 1.0 | 0.0 |
| 3 | 0.096154 | 0.008197 | 0.775510 | 1.0 | 0.0 |
| 4 | 0.250000 | 0.016393 | 0.397959 | 1.0 | 0.0 |
| ... | ... | ... | ... | ... | ... |
| 195 | 0.326923 | 0.860656 | 0.795918 | 1.0 | 0.0 |
| 196 | 0.519231 | 0.909836 | 0.275510 | 1.0 | 0.0 |
| 197 | 0.269231 | 0.909836 | 0.744898 | 0.0 | 1.0 |
| 198 | 0.269231 | 1.000000 | 0.173469 | 0.0 | 1.0 |
| 199 | 0.230769 | 1.000000 | 0.836735 | 0.0 | 1.0 |
وأخيرًا نقوم بعملية تقسيم المجموعات
algorithm = (KMeans(n_clusters = 4 ,init='k-means++', n_init = 10 ,max_iter=300,
tol=0.0001, random_state= 111 , algorithm='elkan'))
algorithm = algorithm.fit(df)
df['Cluster'] = algorithm.predict(df)
df.sample(10)
| Age | Annual Income (k$) | Spending Score (1-100) | Gender_Female | Gender_Male | Cluster | |
|---|---|---|---|---|---|---|
| 90 | 0.961538 | 0.360656 | 0.551020 | 1.0 | 0.0 | 2 |
| 89 | 0.615385 | 0.352459 | 0.459184 | 1.0 | 0.0 | 2 |
| 33 | 0.000000 | 0.147541 | 0.928571 | 0.0 | 1.0 | 1 |
| 144 | 0.134615 | 0.508197 | 0.112245 | 0.0 | 1.0 | 3 |
| 177 | 0.173077 | 0.598361 | 0.693878 | 0.0 | 1.0 | 1 |
| 155 | 0.173077 | 0.516393 | 0.897959 | 1.0 | 0.0 | 0 |
| 128 | 0.788462 | 0.459016 | 0.102041 | 0.0 | 1.0 | 3 |
| 179 | 0.326923 | 0.639344 | 0.908163 | 0.0 | 1.0 | 1 |
| 140 | 0.750000 | 0.491803 | 0.040816 | 1.0 | 0.0 | 2 |
| 79 | 0.596154 | 0.319672 | 0.418367 | 1.0 | 0.0 | 2 |
نصيحة فِهم للتعلم
عند القيام باستخدام خوارزمية التجميع تذكر الآتي
فهم المشكلة والبيانات قبل تطبيق أي خوارزمية تجميع، من المهم أن يكون لديك فهم جيد للمشكلة التي تحاول حلها والبيانات التي تعمل بها. التجميع هو أسلوب استكشافي، لذلك يجب أن يكون لديك فكرة واضحة عما تريد تحقيقه والأفكار التي تأمل في اكتسابها من التحليل.
المعالجة المسبقة للبيانات تعد المعالجة المسبقة للبيانات خطوة مهمة في أي مهمة للتعلم الآلي، وخوارزميات التجميع ليس استثناءً. قد تحتاج إلى التعامل مع القيم المفقودة والقيم المتطرفة ومشكلات القياس قبل تطبيق أي خوارزمية تجميع. تأكد من فهمك لخصائص البيانات ومعالجتها مسبقًا وفقًا لذلك.
اختر الخوارزمية الصحيحة هناك العديد من خوارزميات التجميع المتاحة، ولكل منها نقاط قوتها وضعفها. اختر الخوارزمية الأنسب لمشكلتك وخصائص البيانات.
تقييم النتائج التجميع هو أسلوب تعليمي غير خاضع للإشراف، مما يعني أنه لا يوجد مقياس واضح لتقييم النتائج. ومع ذلك يمكنك استخدام مقاييس مختلفة مثل طريقة الكوع.
استمر في التكرار التجميع هو عملية تكرارية، وقد تحتاج إلى تجربة خوارزميات مختلفة، ولذلك لا تخف من تجربة أساليب مختلفة وكرر الأمر حتى تجد الحل الأفضل.
استخدم المعرفة بالمجال غالبًا ما يكون التجميع أكثر فعالية عندما يقترن بمعرفة المجال. استخدم فهمك للمشكلة والبيانات لتوجيه التحليل وتفسير النتائج بطريقة هادفة. لا تعتمد فقط على خوارزمية التجميع لتقديم رؤى ، بل استخدمها كأداة لزيادة معرفتك وخبراتك.
ماذا تعلمنا؟
-
Clustering algorithms هي خوارزميات غير خاضعة للإشراف تستخدم لتجميع الصفوف المتشابهة في مجموعات
-
تطبيقات خوارزميات التجميع متعددة مثل اكتشاف الأنماط المختلفة في البيانات
-
في درس اليوم قمنا بتقسيم العملاء باستخدام أحد أشهر أنواع التجميع وهو K-Means Clustering
-
يمكننا تقسيم العملاء بناء على ميزتين فقط أو على العديد من المزايا
-
إن اختيار عدد المجموعات (الكلسترز) المناسب يكون من خلال عدة طرق مثل طريقة الكوع المستخدمة في درس اليوم
-
طريقة الكوع هي طريقة لإيجاد الحد الذي لا ينقص بعده القصور الذاتي كثيرًا
-
لابد أن تكون جميع الأعمدة عبارة عن أرقام أو محولة إلى أرقام، ولابد من توحييد المقاييس لكل عمود
نهاية الرحلة
تهانينا! في ختام جزء اليوم نكون قد أكملنا سويًا هذه الرحلة الشيقة مع تعلم الآلة. خلال هذه الرحلة المكونة من ستة أجزاء قمنا بالتدرب على المستوى الأساسي في تعلم تقنية تعلم الآلة من خلال الحصول على المعرفة في تقنيات التعلم الخاضع للإشراف والغير خاضع للإشراف. لقد تعلمنا سويًا عن الخوارزميات المختلفة المستخدمة في هذه الأساليب وكيفية عملها وتطبيقاتها العملية. الآن حان الوقت لرفع مستوى مهاراتك عن طريق المزيد من الممارسة. عن طريق تطبيق ما تعلمته، يمكنك اكتساب المزيد من الخبرة والمعرفة في مفاهيم تعلم الآلة. وبمواصلة الممارسة، ستكتسب فهمًا أعمق لكيفية اختيار الخوارزميات والمعلمات المناسبة لمجموعات البيانات الخاصة بك، وستتمكن من تطوير نماذج أكثر دقة يمكنها القيام بالتنبؤات وكشف الأنماط الخفية في بياناتك مما يجعلك جاهزًا للخطوة القادمة كعالم بيانات.
إن كان لديكم أية استفسارات في مجال التعلم الآلي أو الذكاء الإصطناعي، ففريق فِهم يسعد في تقديم المشورة والعون. وتذكروا أن رحلة التعلم طويلة ولكنها ممتعة. وأن قليل مستمر خيرٌ من كثير منقطع.