مقدمة
أهلا بكم في الجزء الخامس من سلسلة فهم لتعلم الآلة. في هذا الجزء سوف نستكشف سويًا ماهو التعلم الآلي الغير خاضع للإشراف وإحدى أهم استخداماته ألا وهي تقليل أبعاد البيانات. إن التعلم الغير خاضع للإشراف هو نوع من أنواع التعلم الآلي تتعلم فيه الخوارزمية أنماط البيانات الغير مسماة، أي أنها تستكشف الأنماط في جداول البيانات التي لا تحتوي على متغيرات مستهدفة. وإن تطبيقات التعلم الآلي الغير خاضع للإشراف متعددة، فهي تشمل تقسيم العملاء، اكتشاف الشذوذ والقيم المتطرفة، التعرف على الصور، معالجة اللغات وأنظمة الاقتراحات. وفي درس اليوم سوف نتناول أحد أشهر تطبيقات التعلم الآلي الغير خاضع للإشراف، ألا وهو تقليل أبعاد البيانات.
تقليل أبعاد البيانات من خلال تحليل المكونات الرئيسية
Dimensionality Reduction via Principal Component Analysis (PCA)تحليل المكونات الرئيسية هو أحد الأساليب الشائعة في التعلم الغير خاضع للإشراف والذي يستخدم لتقليل الأبعاد. وهو عبارة عن طريقة إحصائية تحدد البنية الأساسية للبيانات ذات الأبعاد الكثيرة - أي التي تحتوي على العديد من الأعمدة - من أجل تقليل حجمها. ولذلك فهي تستخدم في فهم البيانات عالية التعقيد ومن أجل تقليل الوقت المستغرق في تدريب النموذج لأن حجم البيانات يصبح أصغر بعد عملية تحليل المكونات الرئيسية.
ماذا نريد أن نفعل؟
قمنا سابقا في درس
ببناء نماذج تعلم آلة تقوم بتصنيف نوع النشاط البدني الذي يقوم به الإنسان، ولكن إن تمعّنا جيدًا في عدد الأعمدة المستخدمة في تدريب النماذج نجد أننا قمنا باستخدام 563 عمود (ميزة) وهو عددٌ كبير جدًا. وهو ما نلاحظه من حجم البيانات ألا وهو 18.4 ميقابايت. مهمتنا اليوم هو تقليل حجم البيانات من خلال تقليص عدد الأعمدة ومن ثم تدريب نماذج تعلم الآلة من جديد مع المحافظة قدر المستطاع على الأداء.
البيانات المستخدمة في هذا الدرس
في هذا الدرس سوف نستكمل استخدامنا لبيانات حركة جسم الإنسان والتي يمكن تنزيلها من الرابط التالي
ويمكنكم الاطلاع على البيانات من مصدرها الأساسي عن طريق الرابط التالي
import pandas as pd
data = pd.read_csv('https://github.com/AI-MOO/Fihm_Lessons/raw/master/Human_Activity_Recognition_ML/data/test.csv')
data.head()
| | tBodyAcc-mean()-X | tBodyAcc-mean()-Y | tBodyAcc-mean()-Z | tBodyAcc-std()-X | tBodyAcc-std()-Y | tBodyAcc-std()-Z | tBodyAcc-mad()-X | tBodyAcc-mad()-Y | tBodyAcc-mad()-Z | tBodyAcc-max()-X | ... | fBodyBodyGyroJerkMag-kurtosis() | angle(tBodyAccMean,gravity) | angle(tBodyAccJerkMean),gravityMean) | angle(tBodyGyroMean,gravityMean) | angle(tBodyGyroJerkMean,gravityMean) | angle(X,gravityMean) | angle(Y,gravityMean) | angle(Z,gravityMean) | subject | Activity |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
0 | 0.257178 | -0.023285 | -0.014654 | -0.938404 | -0.920091 | -0.667683 | -0.952501 | -0.925249 | -0.674302 | -0.894088 | ... | -0.705974 | 0.006462 | 0.162920 | -0.825886 | 0.271151 | -0.720009 | 0.276801 | -0.057978 | 2 | STANDING |
1 | 0.286027 | -0.013163 | -0.119083 | -0.975415 | -0.967458 | -0.944958 | -0.986799 | -0.968401 | -0.945823 | -0.894088 | ... | -0.594944 | -0.083495 | 0.017500 | -0.434375 | 0.920593 | -0.698091 | 0.281343 | -0.083898 | 2 | STANDING |
2 | 0.275485 | -0.026050 | -0.118152 | -0.993819 | -0.969926 | -0.962748 | -0.994403 | -0.970735 | -0.963483 | -0.939260 | ... | -0.640736 | -0.034956 | 0.202302 | 0.064103 | 0.145068 | -0.702771 | 0.280083 | -0.079346 | 2 | STANDING |
3 | 0.270298 | -0.032614 | -0.117520 | -0.994743 | -0.973268 | -0.967091 | -0.995274 | -0.974471 | -0.968897 | -0.938610 | ... | -0.736124 | -0.017067 | 0.154438 | 0.340134 | 0.296407 | -0.698954 | 0.284114 | -0.077108 | 2 | STANDING |
4 | 0.274833 | -0.027848 | -0.129527 | -0.993852 | -0.967445 | -0.978295 | -0.994111 | -0.965953 | -0.977346 | -0.938610 | ... | -0.846595 | -0.002223 | -0.040046 | 0.736715 | -0.118545 | -0.692245 | 0.290722 | -0.073857 | 2 | STANDING |
5 rows × 563 columns
عند التحقق من عدد الأعمدة نجد أن لدينا 563 عمودًا مستخدما.
print('data dimensions are:', data.shape)
data dimensions are: (2947, 563)
ماهي المشكلة بالأبعاد الكثيرة؟
إن وجود مجموعة بيانات تحتوي على 563 عمودًا قدد يسبب مشاكل في ما يلي
وقت الحساب
مع وجود عدد كبير من الأعمدة، تستغرق معالجة البيانات وتدريب نماذج التعلم الآلي وقتًا أطول.
تشبع النموذج
عندما يكون لدينا الكثير من الميزات، سيكون هناك في الغالب الكثير من الضوضاء (معلومات ذات أهمية قليلة أو معدومة) في البيانات بدلاً من الأنماط الأساسية. وهذا سوف يؤدي إلى زيادة تشبع النموذج، مما يعني أن النموذج سوف يعمل بشكل جيد على بيانات التدريب ولكن بشكل سيئ على البيانات الجديدة كما أشرنا في الجزء الرابع من السلسلة.
لعنة الأبعاد
إن مع زيادة عدد الميزات، تزداد أيضًا كمية البيانات المطلوبة (عدد الصفوف) لتحقيق مستوى مقبول في أداء النموذج. يُعرف هذا بإسم لعنة الأبعاد، ويمكن أن يكون تحديًا خاصةً حين تكون البيانات محدودة.
الحل: لمعالجة هذه المشكلات، يمكن استخدام تقنية تحليل المكونات الأساسية PCA لتقليل عدد الأعمدة في مجموعة البيانات، والتي سوف تساعدنا في التقاط أكبر كمية من المعلومات المفيدة وإزالة المعلومات الزائدة عن الحاجة أو ليست ذات الصلة. مما يؤدي إلى وقت تدريب أسرع، وتقليل مخاطر التشبع العالي (Reducing data dimensions reduces training time and the risk of overfitting).
الخطوة الأولى: قياس وقت التدريب و دقة النموذج على الأبعاد الكاملة
Step One: Measure Time and Accuracy on The Complete Dimensionsنقوم بفصل البيانات أولا كالتالي
X = data.drop('Activity', axis = 1) #Independent variables
y = data.Activity #Dependent variable
from sklearn.model_selection import train_test_split
rs = 221
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=rs, stratify = y)
ومن ثم توحيد المقايس بين الأعمدة
from sklearn.preprocessing import StandardScaler
scalar = StandardScaler()
X_train_s = scalar.fit_transform(X_train)
X_test_s = scalar.transform(X_test)
الآن سوف نستخدم خوازمية الانحدار الخطي لتدريب النموذج ورؤية الوقت المستغرق في التدريب والدقة الناتجة.
للتنويه: عند استخدام نفس الحالة العشوائية (3221) سوف نحصل على نتائج دقة متساوية، ووقت التدريب سوف يختلف باختلاف المعالج المستخدم ولكنه سوف يكون اختلاف طفيف جدًا.
from sklearn.linear_model import LogisticRegression
%%time
model = LogisticRegression(solver='liblinear', random_state = rs)
model = model.fit(X_train_s, y_train)
y_pred = model.predict(X_test_s)
CPU times: user 2.01 s, sys: 15.6 ms, total: 2.03 s Wall time: 2.03 s
نلاحظ أن CPU times = 2.01 s وهو الوقت الذي استغرقه المعالج لتدريب النموذج وإجراء التوقع. الآن فلنقم بالتحقق من الدقة.
from sklearn.metrics import accuracy_score
print('Accuracy score: ', round(accuracy_score(y_test, y_pred), 2))
Accuracy score: 0.98
الخطوة الثانية: تقليل أبعاد البيانات
Step Two: Reduce Data Dimensionsسوف نقوم الآن بتجربة اختزال جميع المزايا المستخدمة ألا وهي 563 إلى ميزتين فقط. ومن ثم تجربة تدريب نموذج على هذه الميزتين فقط ورؤية أثرها في تقليل وقت التدريب وعلى الدقة.
# Reduce dimensions
from sklearn.decomposition import PCA
model = PCA(n_components=2) # Use 2 components only
X_train_s_PCA = model.fit_transform(X_train_s)
X_test_s_PCA = model.transform(X_test_s)
لاحظ أننا قمنا باستخدام الأعمدة المستقلة فقط في تدريب النموذج X_train_s لأننا لا نقوم باستخدام العمود المستهدف y_train في تدريب نماذج التعلم الآلي الغير خاضع للإشراف. ويمكننا التحقق من البعدين الناتجين كالتالي
X_test_s_PCA[1:11]
array([[-15.21833787, 1.1179913 ],
[ 36.00811118, 5.52825821],
[ -1.72974663, -9.75052315],
[-13.87582545, -0.24468543],
[-16.05932873, -3.17572823],
[-16.67426293, 6.54099994],
[-16.8641901 , 1.06662178],
[-16.90179699, 2.07001619],
[-14.55951538, -5.19195412],
[-11.79378466, -6.60872167]])الآن فلنقم بتدريب نموذج التصنيف باستخدام PCA1 & PCA2 فقط ورؤية الوقت المستغرق في التدريب.
%%time
model = LogisticRegression(solver='liblinear', random_state = rs)
model = model.fit(X_train_s_PCA, y_train)
y_pred = model.predict(X_test_s_PCA)
CPU times: user 13.2 ms, sys: 1.02 ms, total: 14.2 ms Wall time: 18.4 ms
نلاحظ أن عملية التدريب قد أصبحت أقصر بكثير، حيث أن الوقت المستغرق لتدريب النموذج وإجراء التوقع أصبح فقط 13.2ms نستطيع حفظ البيانات المختزلة مع العامود المستهدف في جدول ورسمه كالتالي
Reduced_df = pd.DataFrame(y_test)
Reduced_df['PCA1'] = X_test_s_PCA[:,0]
Reduced_df['PCA2'] = X_test_s_PCA[:,1]
Reduced_df.reset_index().drop('index',axis = 1)
Reduced_df.sample(10)
| | Activity | PCA1 | PCA2 |
|---|---|---|---|
1658 | WALKING_DOWNSTAIRS | 29.411444 | 5.817405 |
1888 | SITTING | -12.834180 | -5.050696 |
1324 | WALKING_DOWNSTAIRS | 27.308516 | 10.027629 |
1338 | WALKING_UPSTAIRS | 12.092042 | -9.790183 |
129 | WALKING_DOWNSTAIRS | 28.314707 | 3.364154 |
2002 | WALKING_DOWNSTAIRS | 8.573754 | -5.650178 |
1574 | LAYING | -16.767812 | 2.527772 |
1707 | STANDING | -12.436791 | -6.884028 |
2390 | WALKING_UPSTAIRS | 20.820705 | -3.753692 |
509 | SITTING | -13.267114 | -8.254636 |
import seaborn as sns
import matplotlib.pyplot as plt
sns.lmplot( x = 'PCA1', y = 'PCA2', hue='Activity', data=Reduced_df, fit_reg=False)
plt.title('Human Activities Classification Using 2 PCA Components only')
plt.show()
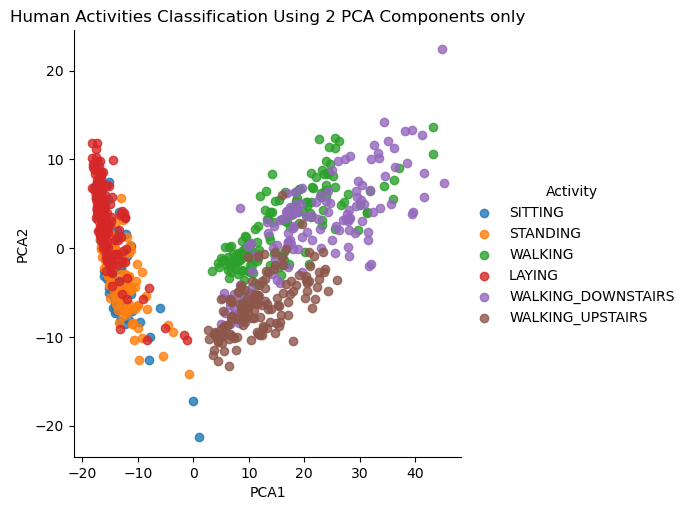
تشير هذه الرسمة الثنائية الأبعاد أننا قمنا بتوقع نوع النشاط البدني الذي يقوم به الإنسان بناء على بعدين فقط ألا وهم PCA1 & PCA2 والآن فلنقم باختبار الدقة كالتالي
print('Accuracy score: ', round(accuracy_score(y_test, y_pred), 2))
Accuracy score: 0.6
نلاحظ أن الدقة متدنية نوعًا ما وغير مرضية. فعلى الرغم من أننا قمنا بتقليل وقت التدريب بشكل ممتاز، إلا أن أداء النموذج سيء. ولتحسين الدقة، فلنقم بتجربة اختزال المعلومات في 20 مكون بدلًا من اثنان فقط ورؤية وقت التدريب مع الدقة الجديدين.
model = PCA(n_components=20) #Reduce data into 20 components
X_train_s_PCA = model.fit_transform(X_train_s)
X_test_s_PCA = model.transform(X_test_s)
%%time
model = LogisticRegression(solver='liblinear', random_state = rs)
model = model.fit(X_train_s_PCA, y_train)
y_pred = model.predict(X_test_s_PCA)
CPU times: user 99 ms, sys: 3.63 ms, total: 103 ms Wall time: 103 ms
print('Accuracy score: ', round(accuracy_score(y_test, y_pred), 2))
Accuracy score: 0.89
حسنًا! لقد قمنا باختزال 563 عامود إلى 20 عامود فقط. وقمنا بالمحافظة نسبيًا على دقة عالية 89% مع تقليل الوقت المستغرق في تدريب واختبار النموذج إلى 99 ملّي ثانية.
الآن سوف نقوم برفع عدد المكونات الرئيسية إلى 200 حتى نستطيع الحصول على مثل الدقة الكاملة وهي 98 بالمئة.
model = PCA(n_components=200)
X_train_s_PCA = model.fit_transform(X_train_s)
X_test_s_PCA = model.transform(X_test_s)
%%time
model = LogisticRegression(solver='liblinear', random_state = rs)
model = model.fit(X_train_s_PCA, y_train)
y_pred = model.predict(X_test_s_PCA)
CPU times: user 936 ms, sys: 9.91 ms, total: 946 ms Wall time: 835 ms
print('Accuracy score: ', round(accuracy_score(y_test, y_pred), 2))
Accuracy score: 0.98
ممتاز! لقد قمنا بنجاح باختزال الأعمدة من 563 إلى 200 عمود فقط و تقليل الوقت الحسابي إلى 936ms فقط مع المحافظة على نفس الدقة.
الخطوة الثالثة: قياس كمية التباين الملتقط
Step Three: Measure the Captured Variance per Componentالآن نحن نتساءلُ سويًا: كيف نختار عدد المكونات المناسب؟ إن عدد المكونات المناسب هو العدد الذي يضمن لنا التقاط كمية التباين الكافية للحصول على الدقة المطلوبة. حيث أن هدف المكونات الرئيسية هو أن تشرح التباين في البيانات، ومفهوم التباين الملتقط يشير إلى النسبة المئوية للتباين الكلي في البيانات التي يتم شرحها من خلال المكونات الناتجة. ولذلك يعد التباين الملتقط مؤشرًا مهمًا لأنه يخبرنا عن مقدار المعلومات الأصلية في البيانات التي تم الاحتفاظ بها بعد إجراء تحليل المكونات الأساسي. ولذلك سوف نقوم برؤية مجموع التباين الملتقط بناء على عدد المكونات الأساسية المستخدمة بدءًا بمكون واحد وصولا إلى 225 مكونا.
import numpy as np
pca_list = list()
feature_weight_list = list()
# Fit a range of PCA models
for n in range(1,226):
# Create and fit the model
PCAmod = PCA(n_components=n)
PCAmod.fit(X) # Remeber that X is the data without the label feature 'Activity'
# Store the model and variance [First principle component always has higher weight]
pca_list.append(pd.Series({'n':n, 'model':PCAmod,
'var': PCAmod.explained_variance_ratio_.sum()})) # pending series to list
# Calculate and store feature importances
weights = PCAmod.explained_variance_ratio_.reshape(-1,1)/PCAmod.explained_variance_ratio_.sum()
overall_contribution = np.abs(PCAmod.components_)*weights
abs_feature_values = overall_contribution.sum(axis=0)
feature_weight_list.append(pd.DataFrame({'n':n,
'features': X.columns,
'values':abs_feature_values/abs_feature_values.sum()}))
pca_df = pd.concat(pca_list, axis=1).T.set_index('n')
display(pca_df.head(10))
display(pca_df.tail(10))
| n | model | var |
|---|---|---|
1 | PCA(n_components=1) | 0.49352 |
2 | PCA(n_components=2) | 0.805745 |
3 | PCA(n_components=3) | 0.830786 |
4 | PCA(n_components=4) | 0.848237 |
5 | PCA(n_components=5) | 0.857658 |
6 | PCA(n_components=6) | 0.865275 |
7 | PCA(n_components=7) | 0.872224 |
8 | PCA(n_components=8) | 0.878073 |
9 | PCA(n_components=9) | 0.883546 |
10 | PCA(n_components=10) | 0.888762 |
| n | model | var |
|---|---|---|
216 | PCA(n_components=216) | 0.998469 |
217 | PCA(n_components=217) | 0.998497 |
218 | PCA(n_components=218) | 0.998524 |
219 | PCA(n_components=219) | 0.998549 |
220 | PCA(n_components=220) | 0.998575 |
221 | PCA(n_components=221) | 0.998601 |
222 | PCA(n_components=222) | 0.998624 |
223 | PCA(n_components=223) | 0.998652 |
224 | PCA(n_components=224) | 0.998674 |
225 | PCA(n_components=225) | 0.998695 |
نلاحظ أن عند استخدام عمودين فقط يتم التقاط 80.05% من التباين، ووصولا إلى 99.87% عند استخدام 225 عمود (أي 225 مكون). يمكننا أيضا رسم التباين الملتقط بناء على عدد المكونات كالتالي
ax = pca_df['var'].plot(kind='line')
ax.set(xlabel='Number of dimensions',
ylabel='Percent explained variance',
title='Explained Variance vs Dimensions');
ax.grid(True)
plt.show()
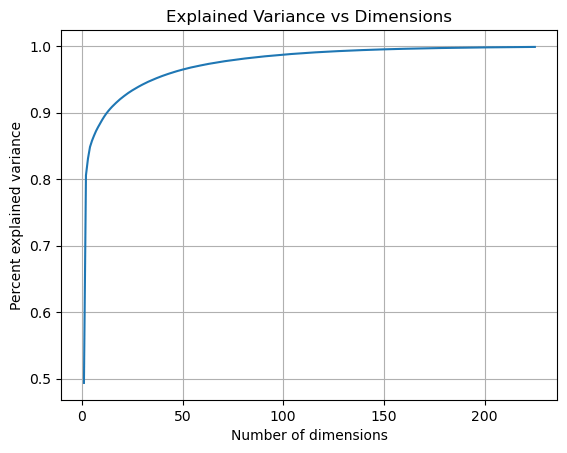
نلاحظ من الرسم البياني أن نسبة التباين الملتقط ترتفع من 80% إلى 95% خلال فترة زيادة أبعاد المكونات الرئيسية من 2 وصولا إلى 50. وبعد ذلك تكون الزيادة طفيفة في مقدار التباين الملتقط. مما يعني أننا نستطيع الحصول على دقة ممتازة إذا تم استخدام 50 مكون أو أكثر.
خطوة إضافية: إيجاد أثر الميزات في التقاط التباين
Bonus Step: Finding Features Impact on Variance Capturingاستنتجنا سويًا أن تحليل المكونات الرئيسية هي تقنية لتقليل أبعاد جدول البيانات مع الاحتفاظ بأكبر قدر ممكن من المعلومات. تتمثل إحدى الفوائد الرئيسية لهذه التقنية في قدرتها على تحديد الميزات (الأعمدة) في جدول البيانات التي لها أكبر مشاركة في كمية التباين الذي تلتقطه المكونات الرئيسية. أي أننا نستطيع أن نستكشف أهمية الميزات بناء على نسبة التباين الذي يقدمه كل عمود. ففي الرسمة السابقة، قمنا برسم كمية التباين الملتقط بناء على عدد المكونات المستخدمة، الأن سوف نقوم بإنشاء جدول يحتوي على كمية المساهمة لكل عمود من الأعمدة المستقلة في نسبة التباين الملتقط كالتالي
features_df = (pd.concat(feature_weight_list)
.pivot(index='n', columns='features', values='values'))
display(features_df.head())
display(features_df.tail())
| features | angle(X,gravityMean) | angle(Y,gravityMean) | angle(Z,gravityMean) | angle(tBodyAccJerkMean),gravityMean) | angle(tBodyAccMean,gravity) | angle(tBodyGyroJerkMean,gravityMean) | angle(tBodyGyroMean,gravityMean) | fBodyAcc-bandsEnergy()-1,16 | fBodyAcc-bandsEnergy()-1,16.1 | fBodyAcc-bandsEnergy()-1,16.2 | ... | tGravityAccMag-arCoeff()4 | tGravityAccMag-energy() | tGravityAccMag-entropy() | tGravityAccMag-iqr() | tGravityAccMag-mad() | tGravityAccMag-max() | tGravityAccMag-mean() | tGravityAccMag-min() | tGravityAccMag-sma() | tGravityAccMag-std() |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
n | |||||||||||||||||||||
1 | 0.000977 | 0.001256 | 0.000118 | 0.000001 | 0.000083 | 0.000017 | 0.001091 | 0.001383 | 0.000892 | 0.000841 | ... | 0.000020 | 0.001561 | 0.004109 | 0.001981 | 0.002407 | 0.002829 | 0.002836 | 0.000999 | 0.002836 | 0.002742 |
2 | 0.001884 | 0.001443 | 0.000854 | 0.000003 | 0.000079 | 0.000114 | 0.000424 | 0.001720 | 0.002247 | 0.001157 | ... | 0.000805 | 0.002093 | 0.005572 | 0.002464 | 0.003083 | 0.003865 | 0.003907 | 0.001417 | 0.003907 | 0.003566 |
3 | 0.002493 | 0.001747 | 0.001025 | 0.000017 | 0.000107 | 0.000113 | 0.000456 | 0.001700 | 0.002206 | 0.001116 | ... | 0.000914 | 0.002058 | 0.005542 | 0.002366 | 0.002966 | 0.003729 | 0.003744 | 0.001355 | 0.003744 | 0.003433 |
4 | 0.002857 | 0.001840 | 0.001131 | 0.000031 | 0.000115 | 0.000137 | 0.000452 | 0.001661 | 0.002150 | 0.001113 | ... | 0.000975 | 0.002007 | 0.005557 | 0.002308 | 0.002891 | 0.003617 | 0.003646 | 0.001326 | 0.003646 | 0.003344 |
5 | 0.002827 | 0.001838 | 0.001152 | 0.000040 | 0.000117 | 0.000139 | 0.000451 | 0.001660 | 0.002229 | 0.001099 | ... | 0.000962 | 0.002014 | 0.005508 | 0.002291 | 0.002862 | 0.003567 | 0.003596 | 0.001306 | 0.003596 | 0.003307 |
5 rows × 562 columns
ولتفسير معنى القيم نلاحظ أن فهرس العمود n يمثل عدد المكونات المستخدمة في كل مرة، فالصف الأول يمثل أن البيانات تم اختزالها في عمود واحد فقط (أي مكون أساسي وحيد). وكل قيمة عمود بالصف تمثل كمية التباين الملتقط من ذلك العمود، ومجموع القيم لكل صف يساوي مجموع نسبة التباين الملتقط. إن هذه التحاليل تساعدنا في معرفة أهمية الميزات وأثرها في عملية إجراء التوقعات، وهذه ميزة أخرى في تحليل المكونات الرئيسية إضافةً إلى قدرتها على تقليل حجم البيانات.
ماذا تعلمنا؟
- في التعلم الغير خاضع للإشراف تبحث الخوارزمية عن البنية الخفية أو العلاقات بين البيانات.
- في التعلم الغير خاضع للإشراف لا يتم استخدام العمود المستهدف.
- قد يستخدم التعلم الغير خاضع للإشراف في تعزيز التعلم الخاضع للإشراف مثل تقليل الوقت المستغرق لتدريب نماذج التصنيف.
- يمكن أن تكون الأبعاد الكبيرة مشكلة في تحليل البيانات والتعلم الآلي.













