مقدمة
أهلا بكم في الجزء الرابع من سلسلة فهم لتعلم الآلة. مازلنا نستكشف سويًا التعلم الآلي الخاضع للإشراف ونرى كيفية استخدامه في حل المشاكل وتطوير الأعمال. اليوم سوف نختبر أثر ضبط عوامل تدريب Hyperparameter Tuning على أداء نماذج تعلم الآلة. حيث أن اختيار عوامل التدريب المناسبة تحسن من عملية تدريب النموذج مما يؤدي لتحسين أداء النماذج وجعلها أكثر دقة. وفي بعض الأحيان ضبط عوامل التدريب يجعل فترة تدريب النماذج أقصر مما يساهم في تقليل تكلفة عملية بناء النماذج. إذاً ماهي عوامل التدريب؟ إن عوامل التدريب هي العوامل التي تحدد كيفية تدريب النماذج، أي أن هي ما تحدد كيفية تشكيل النموذج.
هل عوامل التدريب هي معاملات النموذج؟
إن من الأمور المحيرة في بداية رحلة التعلم على بناء نماذج تعلم الآلة هو التفرقة ما بين معاملات النموذج (Parameters) وما بين عوامل التدريب (Hyperparameters) حيث أن كلاهم عبارة عن عوامل يتم ضبطهم ولكن ما الفرق بينهم؟
» معاملات نموذج تعلم الآلة
هي المعاملات التي تحدد كيفية عمل النموذج في إجراء عملية التوقع. وهي معاملات تتشكل خلال مرحلة تدريب النموذج بناء على البيانات المجمّعة. وللتوضيح أكثر انظر إلى المعادلة العامة للتعلم الآلي الخاضع للإشراف.
المعادلة العامة في التعلم الآلي الخاضع للإشراف: f(\Omega, x) = _p y
x: المدخلات وهي الأعمدة المستخدمة في إجراء التوقع
\Omega: المعاملات التي يحاول النموذج إيجادها خلال عملية التدريب من أجل التوقع بشكل صحيح
_p y: التوقع الناتج بناء على المعاملات والمدخلات
وما تعنيه هذه المعادلة هو أن عملية تدريب نموذج تعلم الآلة هي عملية لإيجاد أفضل المعاملات التي إذا استخدمت مع قيم البيانات (الأعمدة) سوف يقوم النموذج بإجراء التوقع بشكل صحيح في معظم الأحيان. وبحسب الخوارزمية تختلف طريقة تحديد العوامل. ولذلك نستنج أنه في حين ذكر معاملات النموذج (Model Parameters) فإننا نقصد المعاملات التي تستخدم مباشرة في التوقع بناء على قيمة المزايا المستخدمة في التدريب. وهي قيم يتم إيجادها من خلال عملية تدريب النموذج.
» معاملات التدريب
هي معاملات تستخدم لتحديد كيفية تدريب النموذج، أي أنها هي التي تحدد كيفية صناعة معاملات النموذج (Hyperparameters specify how model parameters will be created) وكما أن معاملات النموذج (Model parameters) تختلف باختلاف الخوارزمية المستخدمة. كذلك الحال في عوامل التدريب (Hyperparameters) فإنها تختلف باختلاف الخوارزمية المستخدمة. وهي تختار قبل عملية بدأ التدريب.
لماذا نحتاج ضبط عوامل التدريب؟
لفهم الهدف من ضبط عوامل التدريب علينا فهم أسباب الخطأ في نماذج تعلم الآلة أولا. حيث أن نماذج الآلة لا تصيب التوقع دائما، وعندما تخطئ يكون الخطأ إحدى الأسباب الثلاث التالية:
مراحل تدريب النموذج
لتجنب تدريب النموذج زيادة عن اللزوم أو عدم تدريبه بالشكل كافي. دعونا ننظر إلى مراحل تدريب النموذج كالتالي:
الخلاصة: إن تدريب النموذج يقلل من الانحياز (Bias) مما يرفع من دقة النموذج ولكنه أيضا يرفع التباين (Variance). رفع التباين مقبول إلى حد ما، ولكن إذا تجاوزنا هذا الحد تصبح قيمة التباين جدًا عالية مما يجعل النموذج يخطئ من جديد. هدفنا هو استخدام ضبط عوامل التدريب لوقف التدريب عند الحد المناسب الذي يضمن أقل انحياز ممكن مقابل رفع التباين بشكل معقول.
الانحياز ضد التباين
Bias vs Variance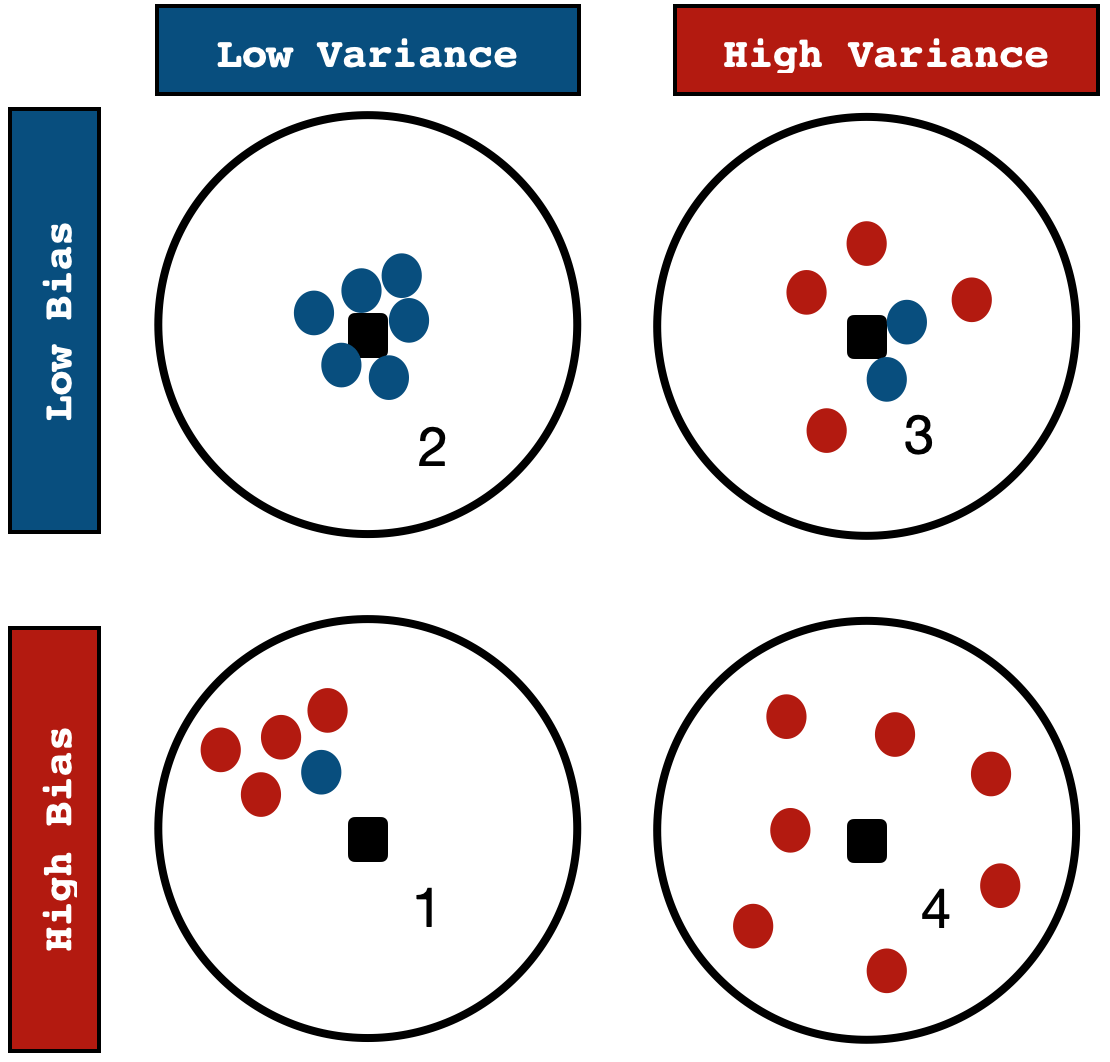
حين النظر إلى الرسمة أعلاه نلاحظ أربعة نماذج يحاولون توقع مكان النقطة السوداء التي بالمنتصف
النموذج الأول هو نموذج تدرب على كمية صفوف قليلة جدًا أو على بيانات منحازة بالأصل ولذلك نجده يقوم بنفس التوقع الخاطئ مرارا وتكرارًا. يسمى هذا النموذج بالنموذج المنحاز (Biased model or underfit model).
النموذج الثاني هو نموذج تم تدريبه على بيانات ذات جودة مناسبة وتم إيقاف تدريبه بالوقت المناسب. ولذلك فإن انحيازه وتباينه قليلين. يسمي هذا النموذج بالنموذج المتزن (Balanced model).
النموذج الثالث هو نموذج تم تدريبه على بيانات ذات جودة عالية ولكن تم تدريبه زيادة عن اللزوم مما جعله نموذج مشبع وأصبحت أخطاؤه كثيره. ولذلك وعلى الرغم من أن هذا النموذج ذو انحياز قليل إلا أن تباينه عالي. يسمى هذا النموذج بالنموذج المعقد (Complex model or overfit model).
النموذج الرابع هو نموذج تم تدريبه بشكل كثيف على بيانات ذات جودة منخفضة. مما جعل تباينه وانحيازه عاليين.
نلاحظ أن أفضل نموذج من ناحية الأداء هو النموذج الثاني حيث أننا استخدمنا بيانات ذو جودة مناسبة وقمنا بتدريب النموذج بشكل كافي، أي أن التدريب لم يكن لفترة قصيرة فيصبح النموذج منحاز ولم يكن لفترة طويلة فيصبح النموذج متبايناً.
الخلاصة: النموذج المناسب هو النموذج الذي يوازن ما بين الانحياز والتباين (A balanced model is a model that balances between bias and variance).
ماذا نريد أن نفعل؟
في درس اليوم سوف نستخدم خوارزمية شجرة القرار (Decision Tree) من أجل تصنيف هل الخلية سرطانية أم لا؟ ثم سوف نقوم باستكشاف الشجرة الناتجة ورؤية كيف تم تكوين الشجرة بناء على عملية تدريب النموذج. بعد ذلك سوف نقوم بضبط عوامل تدريب الشجرة ونرى أثر ذلك على دقة النموذج أولا، وعلى كيفية تغييره لشكل الشجرة ثانيا.
ماهي خوارزمية شجرة القرار؟
خوارزمية شجرة القرار هي خوارزية تقوم بوضع عدة قواعد لعمل التصنيف بناء على البيانات المدخلة. بحيث أن كل قاعدة هي عبارة عن سلسلة من الشروط (if-else) بدءاً بالجذر (Tree Root) ووصولا إلى ورقة الشجرة (Tree Leaf) وكل ورقة شجرة تمثل التصنيف. على سبيل المثال قمنا برسم شجرة قرار لتقييم أداء الطلاب بناء على درجتهم في الاختبار. نلاحظ أن شجرة القرار هي طريقة لمحاكاة المنطق البشري في اتخاذ التصنيف المناسب.
إن سبب اهتمامنا في شكل شجرة القرار هو أن شكل الشجرة تمثل عوامل الشجرة (Tree Parameters) أي أنها تتحدد من خلال عملية التدريب. وكل ما استمرت عملية التدريب على البيانات كلما زاد طول الشجرة وزاد التباين. ولذلك نحن نقوم بضبط عوامل التدريب للتحكم بطريقة تشكيل فروع الشجرة (أي كيفية تشكيل عوامل الشجرة) للحفاظ على قيمة تباين قليلة.
البيانات المستخدمة في هذا الدرس
إن البيانات المستخدمة هي نتائج مختبرية عن عينات ورم ليتم تصنيفها هل الورم حميد أم خبيث بناء على صفات الورم مثل الحجم. إن قيم العمود المستهدف هي:
ويمكنكم تنزيل البيانات من الرابط التالي
import pandas as pd
df = pd.read_csv('https://github.com/KAFSALAH/Fihm_Lessons/raw/master/ML_Series4_Hyperparameters_Tuning/tumor_data.csv')
df.head()
| | Clump | UnifSize | UnifShape | MargAdh | SingEpiSize | BareNuc | BlandChrom | NormNucl | Mit | Class |
|---|---|---|---|---|---|---|---|---|---|---|
0 | 5 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 1 | 0 |
1 | 5 | 4 | 4 | 5 | 7 | 10 | 3 | 2 | 1 | 0 |
2 | 3 | 1 | 1 | 1 | 2 | 2 | 3 | 1 | 1 | 0 |
3 | 6 | 8 | 8 | 1 | 3 | 4 | 3 | 7 | 1 | 0 |
4 | 4 | 1 | 1 | 3 | 2 | 1 | 3 | 1 | 1 | 0 |
الخطوة الأولى: تعريف الوظائف المساعدة
Step One: Defining Auxiliaries Functionsسوف نقوم بتعريف وظيفة تقوم بتقييم أداء النموذج باستخدام المعايير التالية Accuracy, Recall, Precision, F1-score.
from sklearn.metrics import accuracy_score, precision_recall_fscore_support
def evaluate_metrics(yt, yp):
results_pos = {}
results_pos['accuracy'] = accuracy_score(yt, yp)
precision, recall, f_beta, _ = precision_recall_fscore_support(yt, yp, average='binary')
results_pos['recall'] = recall
results_pos['precision'] = precision
results_pos['f1score'] = f_beta
return results_pos
سوف نقوم أيضا بتعريف وظيفة تقوم برسم شجرة القرار بعدما يتم تدريبها
from sklearn import tree
import matplotlib.pyplot as plt
def plot_decision_tree(model, feature_names):
plt.subplots(figsize=(25, 20))
tree.plot_tree(model,
feature_names=feature_names,
filled=True)
plt.show()
وسوف نقوم أيضا بتثبيت الحالة العشوائية في النماذج. والسبب بذلك إننا حينما نقوم باختيار صفوف الاختبار وصفوف التدريب فإننا نختار الصفوف بشكل عشوائي حسب قيمة الحالة العشوائية و التي تتغير في كل مرة. ولضمان إننا سوف نختبر النماذج المختلفة باستخدام نفس الصفوف نقوم بتوحيد الحالة العشوائية (random_state).
rs = 9981 # Setting random state to 9981
ملاحظة: اذا قمت باستخدام 9981 كرقم الحالة العشوائية فسوف تحصل على نفس النتائج التي لدينا. وتستطيع أيضا تجربة أرقام أخرى لرؤية أثرها.
الخطوة الثانية: بناء نموذج شجرة القرار
Step Two: Built A Decision Tree Modelإن أحد مزايا خوارزمية شجرة القرار هو أننا لا نحتاج إلى إعادة وزن الأعمدة (Scaling) ولذلك سوف نقوم بفصل البيانات مباشرة
X = df.drop('Class', axis = 1) # Training features
y = df.Class # Target features
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, stratify=y, random_state = rs)
الآن سوف نقوم ببناء نموذج شجرة قرار بدون ضبط عوامل التدريب والتحقق من أداء النموذج.
from sklearn.tree import DecisionTreeClassifier
plain_model = DecisionTreeClassifier(random_state=rs)
plain_model.fit(X_train, y_train)
preds = plain_model.predict(X_test)
evaluate_metrics(y_test, preds)
{'accuracy': 0.9239766081871345,
'recall': 0.9333333333333333,
'precision': 0.8615384615384616,
'f1score': 0.8960000000000001}نلاحظ التالي: لقد حصلنا على دقة تساوي 92.4% وعلى قيمة إف-ون تساوي 89.6% باستخدام نموذج شجرة القرار بدون ضبط عوامل التدريب.
فلنقم برسم الشجرة لمعرفة كيفية شكلها (كيف تشكلت بناءً على التدريب بالبيانات المزودة).
feature_names = X.columns.values #Taking columns names
plot_decision_tree(plain_model, feature_names)
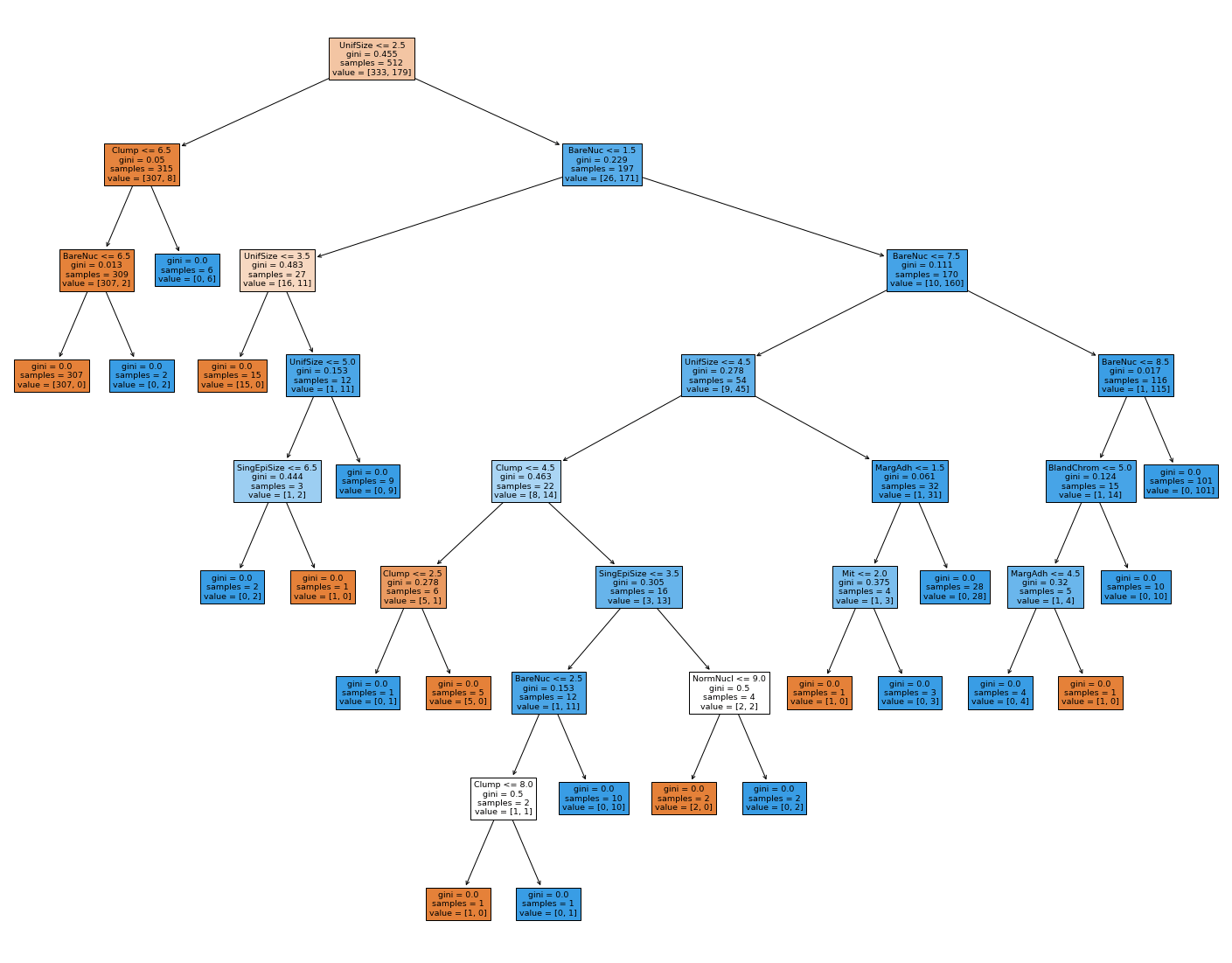
هناك ثلاث ألوان لأوراق الشجرة كالتالي:
الأوراق البرتقالية هي أوراق يكون معظم الصفوف فيها مصنفة على أنها 0 أي أنها أورام حميدة.
الأوراق الزرقاء هي الأوراق التي يكون معظم الصفوف فيها مصنفة على أنها 1 أي أورام خبيثة.
أخيرا الأوراق البيضاء هي الأوراق التي تساوت عدد عينات الأورام الحميدة والخبيثة فيها.
نلاحظ أن شجرة القرار التي نتجت لدينا هي شجرة معقدة نوعًا ما ولديها العديد من التفرعات. تذكر إنه كلما كبرت الشجرة كل ما زاد تعقيدها وأصبحت ذات تباين عالي جدًا (Longer decision trees tend to overfit and have high variance).
الخطوة الثالثة: ضبط عوامل تدريب شجرة القرار
Step Three: Tune Decision Tree Hyperparametersيوجد العديد من عوامل التدريب لشجرة القرار. وللاطلاع عليها قم بتجربة الكود التالي:
# DecisionTreeClassifier?
في درس اليوم، سوف نقوم بتجربة ضبط ثلاثة عوامل تدريب ألا وهم:
سوف نقوم الآن باختبار القيم التالية لعوامل التدريب ورؤية أثرهم على شكل الشجرة وأداؤها
custom_model = DecisionTreeClassifier(criterion='entropy', max_depth=3, min_samples_leaf=3, random_state=rs)
custom_model.fit(X_train, y_train)
preds = custom_model.predict(X_test)
evaluate_metrics(y_test, preds)
{'accuracy': 0.9298245614035088,
'recall': 0.9,
'precision': 0.9,
'f1score': 0.9} نلاحظ أن دقة النموذج قد تحسنت بشكل طفيف 92.98% ونلاحظ ان قيمة ال إف-ون أيضا تحسنت وأصبحت 90%. والآن فلنقم برسم الشجرة كالتالي
plot_decision_tree(custom_model, feature_names)
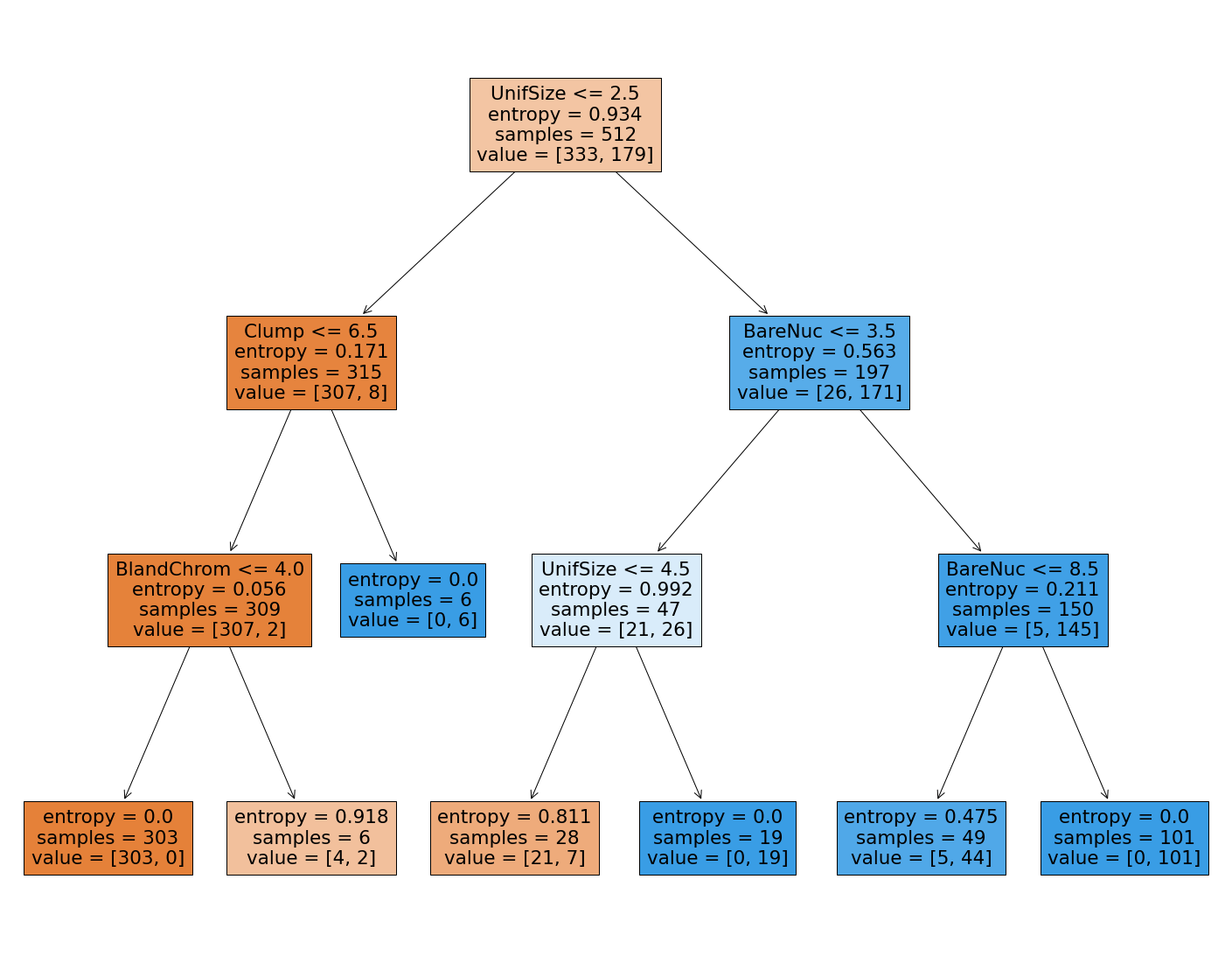
لاحظ كيف أن هذه الشجرة لديها عمق يساوي 3 فقط، وكيف أن الشجرة أصبحت أبسط من السابق وأصبح من السهل تفسيرها. فلنقم الآن بتجربة عوامل مختلفة كالتالي
custom_model = DecisionTreeClassifier(criterion='gini', max_depth=10, min_samples_leaf=3, random_state=rs)
custom_model.fit(X_train, y_train)
preds = custom_model.predict(X_test)
display(evaluate_metrics(y_test, preds))
plot_decision_tree(custom_model, feature_names)
{'accuracy': 0.935672514619883,
'recall': 0.9333333333333333,
'precision': 0.8888888888888888,
'f1score': 0.9105691056910569} 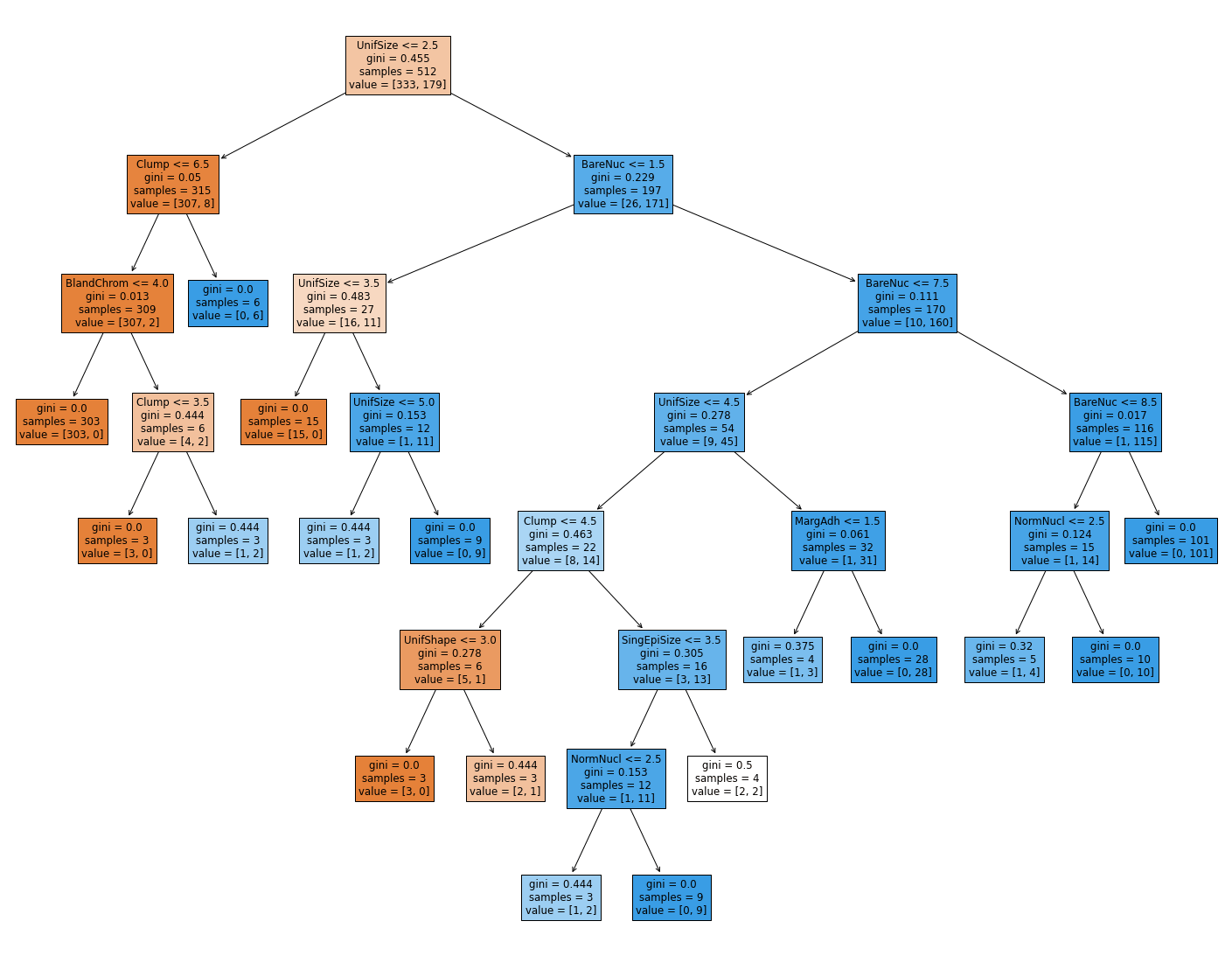
نلاحظ الآن أن هذه الشجرة (الشجرة الثالثة) أعقد من الشجرة الثانية وأبسط من الشجرة الأولى. ولكنها الأعلى من حيث الدقة و الإف- ون سكور. الآن ربما تتسآل هل سوف نقوم بتجربة جميع الاحتمالات يدويا من أجل الوصول إلى أفضل شجرة قرار متزنة؟ ولحسن الحظ لا نحتاج إلى ذلك.
الخطوة الرابعة: استخدام GridSearchCV للحصول على أفضل القيم لضوابط التدريب
Step Four: Use GridSearchCV to find the best HyperparametersGridSearchCV هي وظيفة تقوم باختبار جميع الاحتمالات الممكنة لضوابط التدريب وتسجيل نتائج الأداء لهذه الاختبارات. وبعد ذلك تقوم بإخبارنا بأعلى نتيجة أداء تم تحقيقها وماهي ضوابط التدريب التي استعملت للوصول لتلك النتائج. ولاستخدام GridSeachCV نقوم أولا بتعريف قاموس يحتوي على عوامل التدريب والقيم التي نريد تجربتها.
params_grid = {
'criterion': ['gini', 'entropy'],
'max_depth': [5, 10, 15, 20],
'min_samples_leaf': [1, 2, 5,10]
}
لاحظ أننا نريد اختبار قيمتين من (criterion) وأربع قيم من (max_depth) وأربعة قيم من (min_samples_leaf) مما يعني أننا سوف نقوم بتجربة 2*4*4 = 32 احتمال
لإجراء اختبار الـ GridSearchCV قمنا باستخدام قيمة الـ F1 كمعيار التقييم للنماذج، أي أننا نريد النموذج الذي لديه أعلى قيمة في الإف ون. وقمنا باختيار 5 كعدد الطيات (CV = Cross Validation = 5) أي بمعنى آخر سوف نقوم باختبار كل احتمالية نموذج من الـ32 احتمالية على 5 أجزاء مختلفة من البيانات. أي أن كل نموذج سوف يتم تقييمه خمس مرات وأخذ متوسط التقاييم
from sklearn.model_selection import GridSearchCV
grid_search = GridSearchCV(estimator = DecisionTreeClassifier(random_state=rs), # first introduce the model
param_grid = params_grid, # Second, the dictionary
scoring='f1', # Scoring metric
cv = 5, verbose = 1) # CV value is 5
grid_search.fit(X_train, y_train)
best_params = grid_search.best_params_
Fitting 5 folds for each of 32 candidates, totalling 160 fits
والآن فلنتحقق ماهي أحسن ضوابط تدريب وجدها الـــ GridSearchCV
best_params
{'criterion': 'gini', 'max_depth': 5, 'min_samples_leaf': 1}إذًا فلنقم ببناء نموذج وضبط عوامل التدريب كالتالي
custom_model = DecisionTreeClassifier(criterion='gini', max_depth=5, min_samples_leaf=1, random_state=rs)
# B- fit and evaluate the model
custom_model.fit(X_train, y_train)
preds = custom_model.predict(X_test)
display(evaluate_metrics(y_test, preds))
# C- Display the tree
plot_decision_tree(custom_model, feature_names)
{'accuracy': 0.9415204678362573,
'recall': 0.9666666666666667,
'precision': 0.8787878787878788,
'f1score': 0.9206349206349207}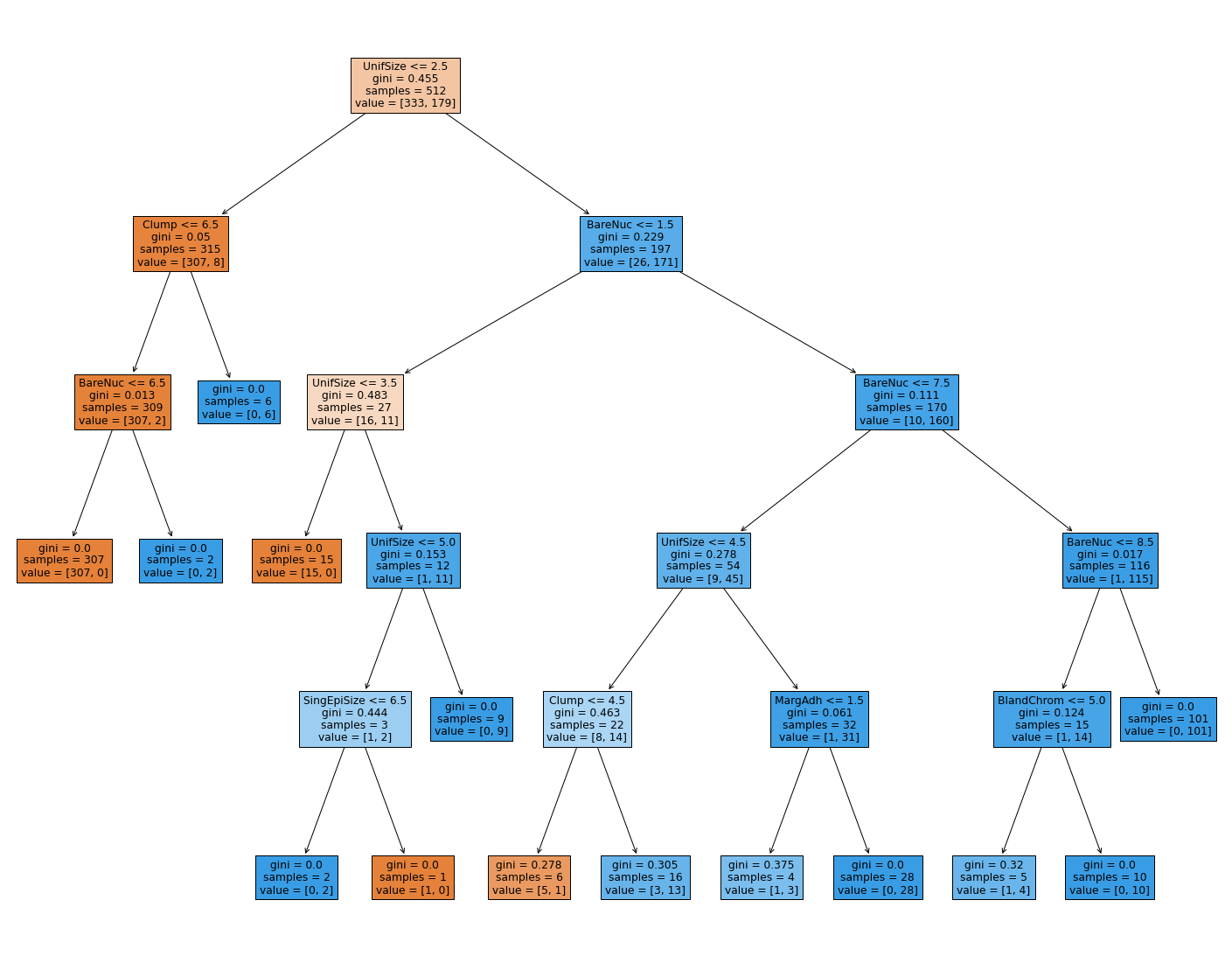
حسنًا، لقد استطعنا بناء نموذج بأعلى قيمة F1 ممكنة، ألا وهي 92% و لاحظ أن الدقة أيضا ارتفعت إلى 94.1% إلا أن الـ Precision قد انخفض إلى 87.87%. تذكر أن تحديد أي معيار لأداء النموذج هو الأهم يختلف باختلاف الهدف من المشروع. وفي مشروع اليوم استطعنا تحقيق هدفنا برفع أداء النموذج بشكل عام عن طريق تحسين قيمة الأف-ون حيث أن الـ F1-score هو معيار شمولي لأداء نماذج التصنيف وقد حصلنا على نتيجة ممتازة.
نصيحة فهم للتعلم
قم باستكشاف عوامل التدريب لخوارزميات مختلفة سواء كانت انحدار خطي أو تصنيف. ثم قم باستخدام GridSearchCV لاستكشاف أفضل عوامل التدريب وقم ببناء النماذج عليها. وصلنا اليوم إلى منتصف الطريق في رحلتنا لتعلم الآلة مع فهم. وخلال هذه الرحلة إلى حد الآن قمنا باستكشاف العديد من المصطلحات والمفاهيم المتعلقة بتعلم الآلة مثل أهمية المزايا، عوامل التدريب، معاير الخطأ وأسباب الخطأ. إن كثرة الأفكار قد تجعلنا في حيرة من أمرنا، وتجعلنا نتساءل العديد من الأسئلة في ما يتعلق باختيار الخطوات المناسبة في بناء النماذج. نصيحتنا في فهم هي الاستمرارية في التدرب والتكرار. حيث أن اتقان تعلم الآلة يتطلب العديد من التجارب، ولذلك كلما بينت نموذج جديد وقمت بتقييمه ومحاولة تحسين أداءه كل ما أصبحت متمرسًا في اختيار الخوارزميات المناسبة وكيفية استخدامها.
ماذا تعلمنا؟
- هناك مصطلحان يجب التفرقة بينهم ألا وهما عوامل النموذج وعوامل تدريب النموذج Parameters vs Hyperparameters
- عوامل النموذج إما أن تكون شكل النموذج مثل شجرة القرار أو معاملات المتغيرات مثل الانحدار الخطي اللوجستي
-
عوامل تدريب النموذج تحدد كيفية تدريب النموذج (أي أنها تحدد كيفية تشكيل عوامل النموذج)
Hyperparameters specifies how parameters will be formulated - عوامل تدريب النموذج تختلف باختلاف الخوارزم
- يمكن تجربة مزيج عوامل نموذج مختلفة دفعة واحدة عن طريق GridSeachCV












