مترجم بتصرف من هذه التدوينة

في هذا المقال سيتم تفصيل خصائص التوزيع للمشتقات الموجهة Histogram of Oriented Gradients والتي تعرف اختصارا بخاصية HOG. سيتم التطرق إلى تفاصيل عمل هذا الواصف وطريقة حسابه باستخدام بعض الحزم الجاهزة مثل OpenCV او استخدام الماتلاب

ماهو واصف الخصائص؟

واصف الخصائص هو عبارة عن تمثيل لصورة او جزء مستقطع من صورة بحيث يقوم بتبسيط الصورة عن طريق استخراج المعلومات المفيدة منها فقط والتخلص من المعلومات الغير مفيدة. بشكل تقليدي يمكن القول بأن واصف الخصائص يقوم بتحويل صورة بحجم (العرضxالطولx ٣ قنوات لونية) إلى فيكتور خصائص (مصفوفة
طولها n).

وعلى سبيل التوضيح لو افترضنا انه لدينا صورة بحجم ٦٤x١٢٨x٣ سيكون الناتج عبارة عن فيكتور خصائص طوله
٣٧٨٠ (سيتم شرح طريقة حساب طول الفيكتور في الخطوة الخامسة).

الجدير بالذكر بأن واصف HOG يمكن حسابه لأحجام مختلفة لكننا في هذا المقال سنلتزم بالاعداد المذكورة في الورقة البحثية الأصلية لفكرة HOG وبالتالي سيكون من السهل استيعاب المفهوم الأساسي بمثال قوي.

نعود الآن لمعرفة ماهي المعلومات المفيدة والغير مفيدة في اي صورة؟ عندما نتحدث عن المعلومات المفيدة فإننا بالتأكيد لانتحدث عن المعلومات المفيدة لاستعراض الصورة! بل إننا نتحدث عن تلك المعلومات المفيدة
لتحديد وتمييز الكائنات في الصورة. بالتالي فإن فيكتور الخصائص المستخرج سيتم تقديمه إلى احد خوارزميات التصنيف مثل SVM لاستنتاج نتائج ممتازة.

ولكن ماهي الخصائص المفيدة لعملية التصنيف؟ سنناقش هذه النقطة باستعراض مثال: لنفترض انك ستقوم ببناء محدد كائنات يقوم بتحديد الازارير في الاقمصة والجاكيتات. الازرار عبارة عن دائرة (قد يظهر بشكل بيضاوي في بعض الصور) وبالعادة يكون فيه بعض الفتحات لعملية الخياطة. وبالتالي من السهل تنفيذ محدد الحواف على الصورة  لتحديد الازرار بمجرد النظر الى الحواف في الصورة. في هذه الحالة، فإن معلومات الحواف هي المعلومات المفيدة بينما معلومات الالوان غير مفيدة. اضف إلى ذلك ان الخصائص المستخرجة يجب ان تكون لديها قدرة التمييز بين الزر وبين اي شكل دائري اخر مثل النقود المعدنية او كفرات السيارة في الصورة.

كيفية حساب خصائص HOG

في هذا الجزء من المقال سيتم تفصيل طريقة حساب خصائص HOG وتقديمه باستخدام صورة محددة على عدة خطوات

الخطوة الأولى: التجهيز Preprocessing

تم استحداث واصف الخصائص HOG في الاساس لغرض تحديد المشاة في الصورة بحيث يتم احتساب HOG على جزء مستقطع من الصورة بحجم ٦٤x١٢٨. وكما تم ذكره سابقا فإنه من الممكن ان يكون حجم الجزء المستقطع من الصورة مختلف عن الذي سيتم تطبيقه في هذا المقال. في العادة يمكن ان يكون الجزء المستقطع يندرج تحت عدة مقاسات في مواقع مختلفة من الصورة ولكن الشرط الوحيد هو ان تكون نسبة العرض الى الارتفاع ثابتة في الجزء المستقطع. في مثالنا في هذا المقال ستكون نسبة العرض للارتفاع هي ١:٢ وهذا يعني ان الجزء المستقطع قد يكون بحجم ١٠٠x٢٠٠ او ١٢٨x٢٥٦ او ١٠٠٠x٢٠٠٠ ولكن ١٠١x٢٠٥ لن يكون خيار صحيح.
لإستوضاح النقطة بشكل افضل فإن شكل(١) يستعرض صورة كبيرة بحجم ٧٢٠x٤٧٥ ومن هذه الصورة تم استقطاع جزء بحجم ١٠٠x٢٠٠ لحساب واصف الخصائص HOG. هذا الجزء المستقطع من الصورة يتم تغيير حجمه إلى ٦٤x١٢٨ وبذلك يصبح جاهزاً لحساب HOG منه.

ورقة البحث الاصلية التي قدمت طريقة HOG ذكرت مايسمى بـ (تصحيح جاما) كخطوة من خطوات التجهيز preprocessing ولكن تنفيذ هذه الخطوة يعطي نتائج طفيفة وبالتالي فسنقوم بتجاهل هذه الخطوة.

الخطوة الثانية: حساب مشتقات الصورة

لحساب واصف HOG نحتاج في البداية إلى حساب المشتقات الطولية والافقية. بعد ذلك سنقوم بحساب التوزيع لهذه المشتقات (histogram of gradients). يتم ذلك ببساطة عن طريق استخدام المرشحات التالية في شكل(٢):

يمكننا ايضا الوصول لنفس النتائج باستخدام معامل Sobel في مكتبة OpenCV حيث ان حجم الخطوة التمريرية يساوي ١

// C++ gradient calculation.
// Read image
Mat img = imread("bolt.png");
img.convertTo(img, CV_32F, 1/255.0);

// Calculate gradients gx, gy
Mat gx, gy;
Sobel(img, gx, CV_32F, 1, 0, 1);
Sobel(img, gy, CV_32F, 0, 1, 1);

او باستخدام بايثون

# Python gradient calculation 
# Read image
im = cv2.imread('bolt.png')
im = np.float32(im) / 255.0

# Calculate gradient
gx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=1)
gy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=1)

بعد ذلك يمكننا ايجاد حجم واتجاه المشتقات باستخدام المعادلة التالية:

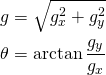
اذا كنت تستخدم OpenCV بإمكانك اجراء الحسابات اعلاه باستخدام دالة csrtToPolar كما هو واضح في الكود ادناه:

// C++ Calculate gradient magnitude and direction (in degrees)
Mat mag, angle;
cartToPolar(gx, gy, mag, angle, 1);

نفس الكود المستخدم في البايثون كالتالي:

# Python Calculate gradient magnitude and direction ( in degrees )
mag, angle = cv2.cartToPolar(gx, gy, angleInDegrees=True)

الشكل التالي شكل(٣) يوضح المشتقات:

لاحظ ان مشتقة-x تعمل على الخطوط الطولية بينما مشتقة-y تعمل على الخطوط الافقية اما حجم المشتقات فيعمل على اي مكان يظهر فيه تغيير حاد في الكثافة. الجدير بالذكر ان جميع المشتقات المذكورة لاتعمل في حالة كانت المنطقة مسطحة او سلسة. لقد تعمدت استبعاد الصورة التي توضح الاتجاه لأن الاتجاه الموضح كصورة لا ينقل الكثير.

الان نرى ان الصورة المشتقة حذفت الكثير من المعلومات الغير مفيدة مثل الوان الخلفية ولكنها قامت بتحديد الحدود. بمعنى اخر يمكننا النظر الى الصورة المشتقة الان واستنتاج بأن هنالك شخص في الصورة بسهولة.
لكل بكسل المشتقة تحتوي على قيمتان: الحجم magnitude والاتجاه direction. بالنسبة للصور الملونة فإن المشتقات للقنوات اللونية الثلاثة يتم تقييمها كما في شكل(٣). قيمة الحجم magnitude للمشتقة في البكسل هي اعلى قيمة للحجم magnitude للمشتقة مابين الثلاث قنوات. اما الزاوية او الاتجاه فيتم تحديدها بناء على اعلى قيمة اشتقاق.

الخطوة الثالثة: حساب التوزيع للمشتقات Histogram of Gradients في خلايا بحجم ٨x٨

في هذه الخطوة يتم تقسيم الصورة المستقطعة إلى خلايا بحجم ٨x٨ شكل(٤) ثم يتم احتساب التوزيع للمشتقات لكل خلية

شكل(٤): تقسيم الصورة المستقطعة إلى خلايا بحجم ٨x٨ (تم تكبير الصورة للتوضيح)

احد الاسباب الاساسية لتقسيم الصورة المستقطعة إلى خلايا بحجم ٨x٨ هو لاننا نريد استخلاص تمثيل مكثف لهذه الصورة وحيث ان الخلية الواحدة بحجم ٨x٨ بكسل فهذا يعني انها تحتوي على ٨x٨x٣ = ١٩٢ قيمة بكسلية. واذا وضعنا بالاعتبار ان مشتقات هذه الصورة المستقطعة تحتوى على قيمتان كما تم شرحه سابقا (الحجم magnitude والاتجاه direction) لكل بكسل فهذا يضيف لنا ٨x٨x٢ = ١٢٨ عدد. بنهاية هذا الجزء سنرى كيف ان الـ ١٢٨ عدد يتم تمثيلها باستخدام ٩صناديق توزيعية (9-bin histogram) والتي يمكن تخزينها في مصفوفة مكونة من ٩ اعداد. بهذه الطريقة سيكون تمثيل الصورة المستقطعة بطريقة مكثفة ومضغوطة بالاضافة إلى ان حساب التوزيع histogram على الصور المستقطعة سيجعل التمثيل مقاوم للتشويش في الصورة. المشتقات الفردية قد تحتوي على تشويش ولكن التوزيع histogram على خلايا بحجم  ٨x٨ يجعت التمثيل اقل حساسية للتشويش.
ولكن لماذا حجم الخلايا ٨x٨؟ لماذا لاتكون ٣٢x٣٢؟ هذا يعتبر خيار للتصميم حسب المقاييس للخصائص التي نبحث عنها، وكما تم ذكره سابقاً فإن HOG تم استخدامها في الاستاس لتحديد المشاة فكانت الخلايا بحجم ٨x٨ للصور المستقطعة للمشاة التي تم تغيير حجمها إلى ٦٤x١٢٨ كبيرة وكافية لالتقاط الخصائص المهمة مثل الوجه واعلى الرأس … الخ.
التوزيع histogram هو عبارة عن فيكتور (او مصفوفة) مكونة من ٩ صناديق (اعداد) بحيث كل صندوق يمثل زاوية معينة: ٠، ٢٠، ٤٠، ٦٠، ٨٠، ١٠٠، ١٢٠، ١٤٠، ١٦٠
شكل(٥) يوضح خلية واحدة بحجم ٨x٨ من الصورة المستقطعة ويمكنك رؤية المشتقات المستخرجة بقيمها الاثنان (الحجم magnitude والاتجاه direction).

اذا كنت مبتدئ في مجال رؤية الكمبيوتر Computer Vision فإن الصورة في المنتصف في شكل(٥) هي صورة مليئة بالمعلومات المفيدة حيث تظهر الاسهم اتجاه الاختلافات اللونية بالاضافة إلى ان طول السهم يمثل الحجم magnitude. لاحظ كيف ان اتجاه السهم يشير الى اتجاه التغيير في الكثافة، اما الحجم (طول السهم) magnitude فيشير إلى مقدار الاختلاف.
في شكل(٥) في الجزء الايمن يمكننا رؤية تمثيل قيم الاشتقاق في الصفوف لكل من الحجم magnitude والاتجاه. يمكن ملاحظة ان الزوايا يتم تسجيلها مابين الصفر و ١٨٠ درجة بدلا من الصفر و ٣٦٠ درجة وهذا مايسمى بالاشتقاق المطلق او الخالي من الاشارة unsigned gradients لان المشتقة ومقابلها السالب يتم تمثيلهم بنفس العدد. بمعنى اخر، سهم الاشتقاق والشئ المعاكس له ب ١٨٠ درجة يتم اعتبارهم متساويين. ولكن لماذا لانستخدم ٠-٣٦٠ درجة؟ بشكل عام فقد ظهر بأنه من الافضل استخدام الاشتقاق المطلق الخالي من الاشارات بدلا من الاشتقاق المصحوب باشارات لتحديد المشاة. بعض التطبيقات لـ HOG قد تسمح لك بتحديد ما اذا كنت تريد استخدام الاشتقاق المصحوب بالاشارات ام لا.
الخطوة التالية هي إنشاء التوزيع histogram للمشتقات في هذه الخلايا حيث ان histogram يحتوي على ٩ صناديق كما ذكرنا مسبقاً وكل صندوق يمثل زاوية معينة من الصفر إلى ١٦٠. شكل(٦) يمثل هذه العملية. بالنظر إلى قيمة الحجم magnitude والاتجاه direction للمشتقات لنفس الخلية بحجم ٨x٨ فإنه يمكن تحديد الصندوق بناء على الاتجاه direction والتصويت (القيمة التي ستكون في الصندوق) يتم اختياره بناء على الحجم magnitude. لنبدأ بالبكسل المحاط باللون الازرق في شكل(٦): البكسل لديه زواية بقيمة ٨٠ درجة (تمثل الاتجاه direction) والحجم magnitude بقيمة تساوي ٢ وبالتالي فإننا نضع العدد ٢ في الصندوق الخامس والذي يمثل الزاوية ٨٠. اما البكسل المحاط باللون الاحمر في شكل(٦) فإن لديه الزاوية ١٠ درجات والحجم magnitude بقيمة ٤. وبما ان الزاوية ١٠ تعتبر في منتصف الطريق بين الزاوية صفر والزاوية ٢٠ يتم تقسيم قيمة التصويت (magnitude) بالتساوي بين الصندوق الاول والثاني.

هنالك شئ اخير يجب معرفته وهو اذا كانت الزاوية اكبر من ١٦٠ درجة (يعني انها تقع مابين ١٦٠ و ١٨٠) فنحن كما نعلم مسبقاً بأن الزاوية سيتم التفافها بحيث تكون متساوية في الصفر و ١٨٠. وفي المثال التالي في شكل(٧) فإن البكسل المحاط بالاخضر لديه زاوية بقيمة ١٦٥ درجة وبالتالي فإن قيمة الحجم magnitude والتي تساوي ٨٥ في هذا المثال ستيم توزيعها بشكل تناسبي مع صندوق الزاوية صفر وصندوق الزاوية ١٦٠.

يتم تجميع كل قيم البكسلات في الخلايا بحجم ٨x٨ لانشاء histogram بتسعة صناديق. وبالنسبة للصورة المستقطعة اعلاه فإن الـ histogram سيظهر بالشكل التالي شكل(٨):

في التمثيل البياني السابق، المحور y عبارة عن زاوية صفر ويمكننا ملاحظة ان الـ histogram لديه الكثير من التركيز بالقرب من الزاوية صفر والزاوية ١٨٠ وهي طريقة اخرى لقول ان المشتقات تتجه اما للاعلى او للاسفل.

الخطوة الرابعة: التسوية Normalization بكتلة بحجم ١٦x١٦

في الخطوة السابقة تم انشاء التوزيع histogram بناء على مشتقات الصورة. هذه المشتقات حساسة للاضاءة بشكل عام. اذا اردنا تعتيم الصورة يمكننا فعل ذلك بقسمة قيم البكسلات جميعها على ٢ وبالتالي فإن قيم الحجم magnitude للمشتقات ستتغير الى النصف وبالتالي فإن قيم histogram ستتغير كذلك الى النصف. ولكننا بشكل عملي نريد ان يكون الواصف لدينا مستقل عن اي تغيير في الاضاءة. بمعنى اخر فإننا نريد القيام بتسوية normalize التوزيع histogram بحيث لا يتأثر بأي تغييرات في الاضاءة.
قبل ان ندخل في شرح طريقة تسوية histogram، دعنا نرى كيف يمكننا تسوية فيكتور بطول ٣:لنفترض بأنه لدينا فيكتور ملون RGB [١٢٨، ٦٤، ٣٢]. طول الفيكتور يتم احتسابه عن طريق معيار L2 باستخدام المعادلة التالية

قسمة كل عدد في الفيكتور على العدد ١٤٦.٦٤ يعطينا الفيكتور بعد التسوية normalized vector [٠.٨٧، ٠.٤٣، ٠.٢٢]. الان لنفترض ان لدينا فيكتور جديد قيمته هي ضعف قيمة الفيكتور الاول [٢٥٦،١٢٨،٦٤] وبالتالي فعند حساب الفيكتور بعد التسوية بنفس الطريقة اعلاه فإننا سنحصل على [٠.٨٧، ٠.٤٣، ٠.٢٢] وهو مطابق تماما للفيكتور المسوى او المعدل للفيكتور الاول وهذا يعني ان عملية التسوية normalization تقوم بحذف المقياس النسبي.
الان وبعد معرفة طريقة تسوية فيكتور فربما قد تكون فكرت بمحاولة تطبيق نفس المفهوم خلال عملية حساب HOG عن طريق تسوية الـ histogram  بحجم ٩x١ بنفس الطريقة التي قمنا فيها بتسوية الفيكتور بحجم ٣x١ اعلاه، وهي فكرة ليست سيئة ولكن من الافضل عمل التسوية normalization باستخدام كتلة بحجم اكبر ١٦x١٦ بحيث ان هذه الكتلة تحتوي على ٤ histograms والتي من الممكن ربطها ببعض لتكون فيكتور بحجم ٣٦x١ (4 histograms x 9bin). ثم بإمكاننا تطبيق عملية التسوية normalization بنفس الطريقة التي استخدمناها مع الفيكتور بحجم ٣x١. ستتحرك النافذة بـ ٨ بكسلات (انظر الصورة المتحركة في شكل(٩)) وبالتالي فإنه يتم حساب الفيكتور المسوى او المعدل بحجم ٣٦x١ بحجم هذه النافذة ويتم تكرار الخطوة حتى الانتهاء من الصورة المستقطعة.

الخطوة الخامسة: حساب فيكتور الخصائص HOG

لحساب فيكتور الخصائص النهائي لكامل الصورة المستقطعة فإن جميع الفيكتور التي تم حسابها بحجم ٣٦x١ يتم ربطها ببعض لتكون فيكتور واحد ضخم. ماهو حجم الفيكتور النهائي؟ سنقوم بحسابه كالتالي:

1. كم عدد المناطق التي تمر عليها كتلة ١٦x١٦؟

لدينا ٧ مناطق افقية و١٥ منطقة عمودية وبالتالي فإن المجموع سيكون ٧x١٥ = ١٠٥ منطقة

2. كل كتلة بحجم ١٦x١٦ يتم تمثيلها بفيكتور بحجم ٣٦x١ وبالتالي فعند ربط جميع الفيكتور التي قمنا باستخراجها في فيكتور واحد ضخم فهذا يعني ٣٦x١٠٥ = ٣٧٨٠ (فيكتور بعدد ابعاد ضخم يساوي ٣٧٨٠)

تصوير خصائص التوزيع للمشتقات الموجهة HOG؟

عادة يتم تصوير واصف HOG باستخدام histogram المسوى او المعدل بحجم ٩x١ في الخلايا بحجم ٨x٨. انظر شكل(١٠) وستلاحظ ان الاتجاه الغالب في التوزيع يحدد شكل الشخص في الصورة بالأخص عند الجذع والساق.
للأسف لايوجد طريقة سهلة لتصوير خصائص التوزيع للمشتقات الموجهة في OpenCV.

تم ترجمة هذا المقال ببعض من التصرف حيث ان كل الصور والرسومات تم جلبها من المقال الأصلي والذي يمكن الوصول اليه من هنا